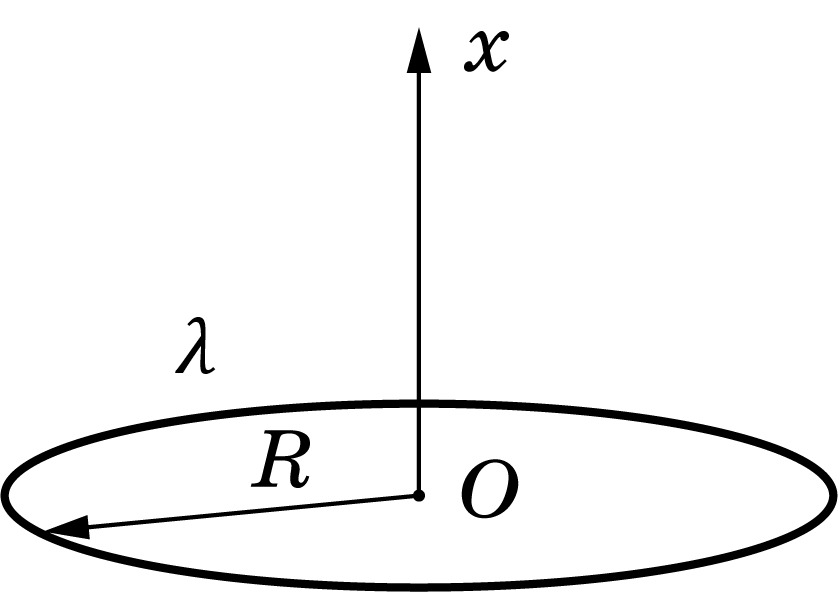
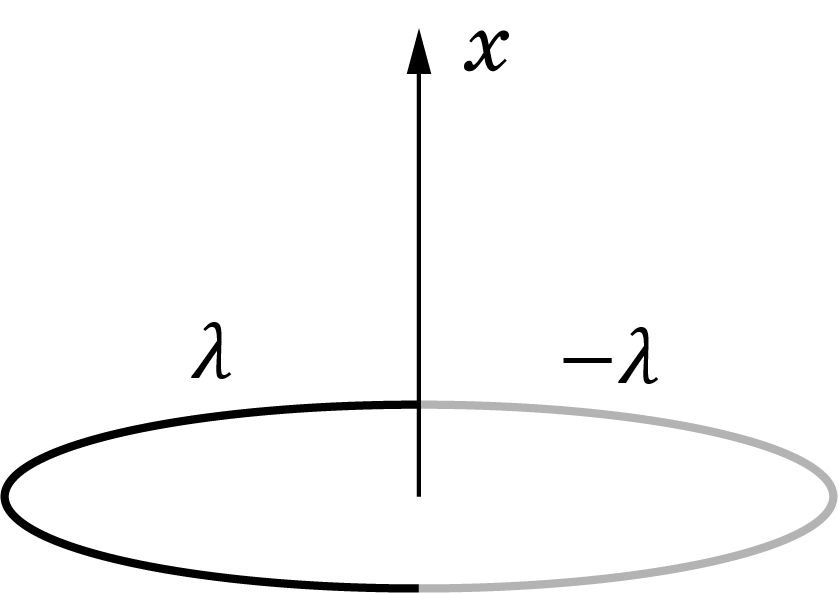
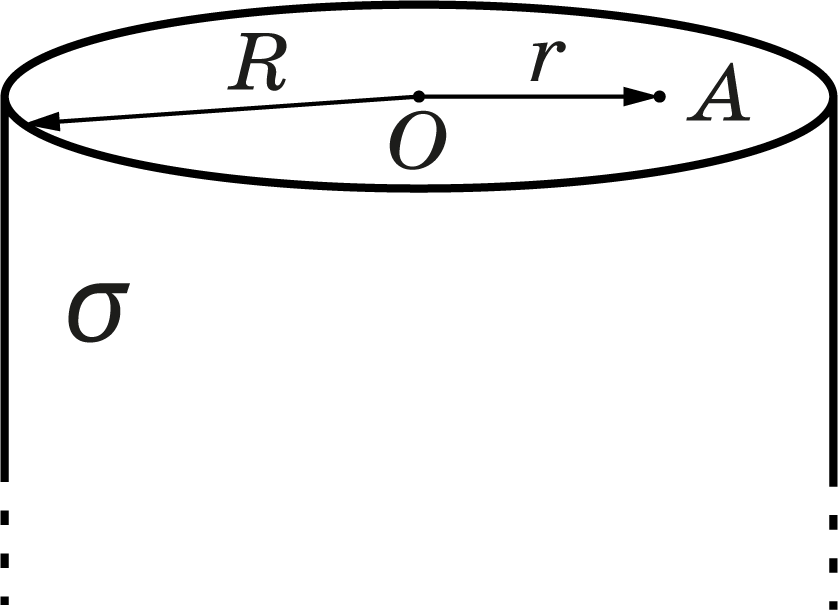
Бесконечный цилиндр радиуса $R$ равномерно заряжен по боковой поверхности с поверхностной плотностью заряда $\sigma$.
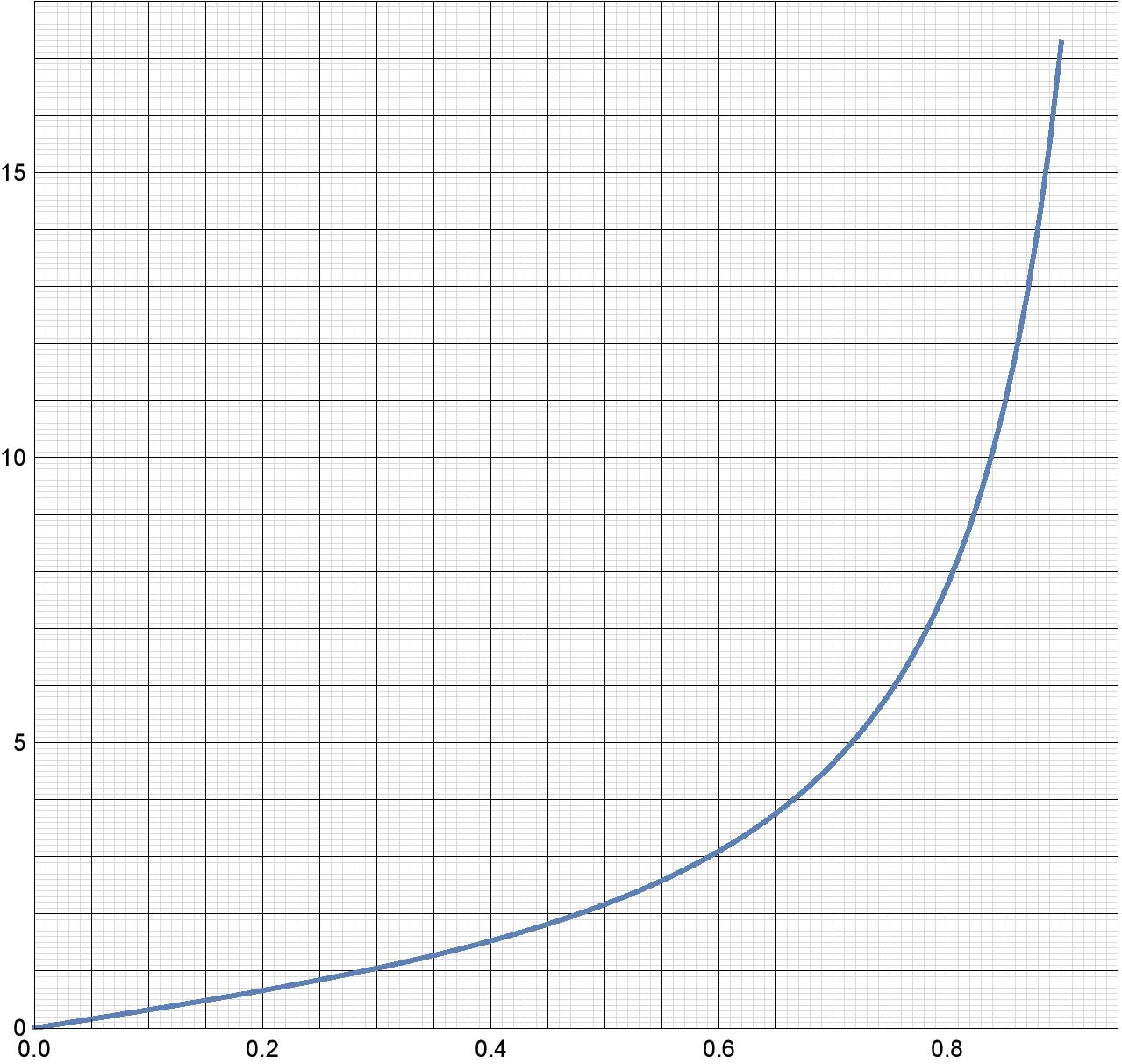
Для решения следующего пункта вам может понадобиться зависимость радиальной компоненты напряженности поля кольца в его плоскости. Если кольцо радиуса $R$ равномерно заряжено зарядом $Q$, то на расстоянии $r$ от его центра радиальная компонента напряженности поля равна
$$E_r=\frac{kQ}{2{\pi}R^2}\cdot y(x)$$
где $x=r/R$. График зависимости $y(x)$ представлен на рисунке ниже.