Часть A. Равноускоренное падение (0.8 балла)

Для начала, пренебрегая эффектом <<фонтана>>, предположим, что наполняющая стакан цепочка бус просто переваливается через его край, и нижний конец цепочки ускоренно спускается. Выпавшие из стакана звенья цепи связаны друг с другом, поэтому импульс силы тяжести расходуется не только на ускорение выпавших звеньев, но и на присоединение новых звеньев к падающей массе, и ускорение получается меньше, чем $g$.

А1  ^0.80 Найдите ускорение нижнего конца цепи, если известно, что оно постоянно.

Часть B. Классика (2.5 балла)

B1  ^0.30 Считая, что потери механической энергии звеньев происходят только при ударе их о пол, а всё предыдущее время механическая энергия сохраняется, найдите скорость $v$ установившегося равномерного движения цепи.

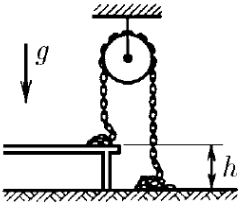
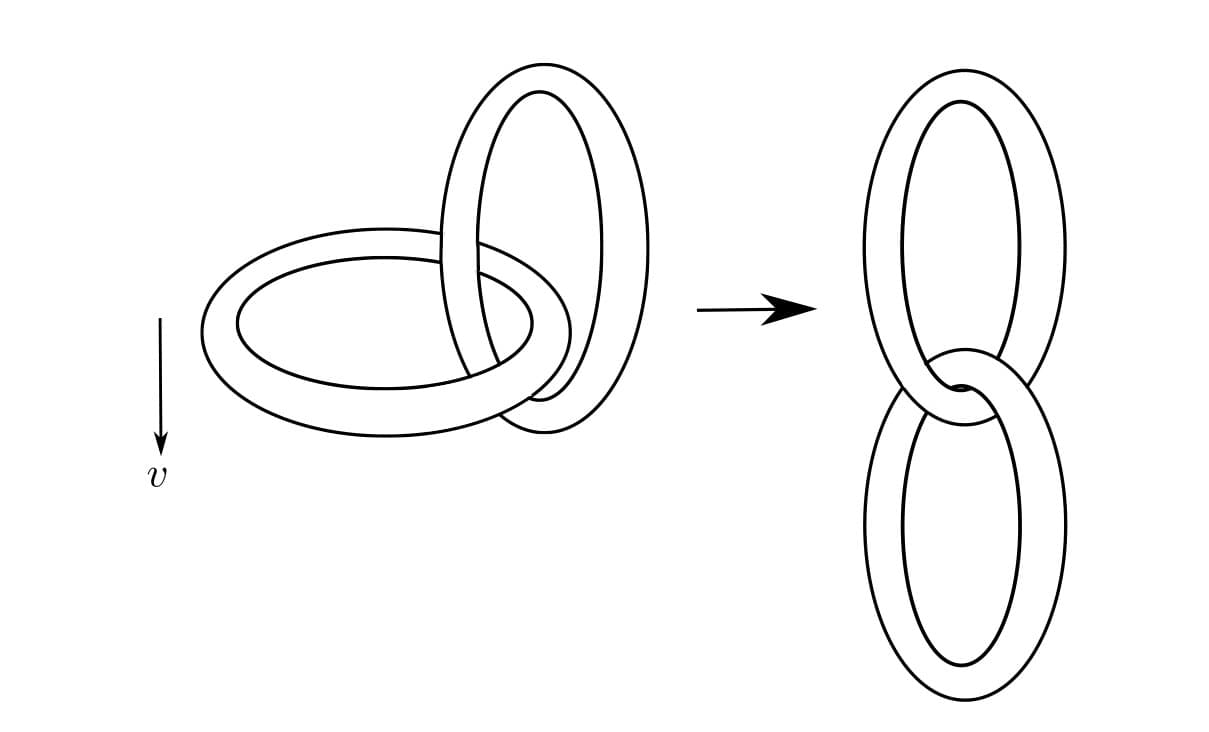
Для проверки сохранения механической энергии при отрыве звеньев от стола решим задачу иным путём: используя закон изменения импульса.

B2  ^0.50 Чему равно натяжение цепи $T_f$ в точках, подлетающих к полу? Каково натяжение цепи $T(h)$ в точках, находящихся на $h$ выше уровня пола? Одинаково ли натяжение в находящихся на одинаковой высоте точках левого и правого отрезков цепи?

B3  ^0.50 Запишите закон изменения импульса и рассчитайте силу натяжения $T_t$ в точках цепи, близких к уровню стола. Ответ выразите с использованием $v$.

B4  ^0.20 Опираясь на результаты пунктов B2 и B3, выразите искомую скорость $v$.

Приступим к анализу энергетических потерь в системе.

B5  ^0.20 Какая механическая энергия за единицу времени $\cfrac{\Delta W_f}{\Delta t}$ переходит в тепло при неупругих ударах упавших звеньев о пол?

B6  ^0.50 Рассчитайте потери механической энергии за единицу времени $\cfrac{\Delta W_t}{\Delta t}$ при неупругих ударах новых звеньев об уже взлетевшие.

B7  ^0.10 Найдите отношение $\cfrac{\Delta W_t}{\Delta W_f}$ потерь энергии на столе и на полу.

B8  ^0.20 Если рассмотреть одни и те же звенья ДО их отрыва от стола и ПОСЛЕ их преземления на пол, то можно рассчитать изменение их потенциальной энергии. Покажите, что оно совпадает с суммой потерь на столе и на полу.

Часть C. Верхняя оценка высоты <<фонтана>> (2.0 балла)

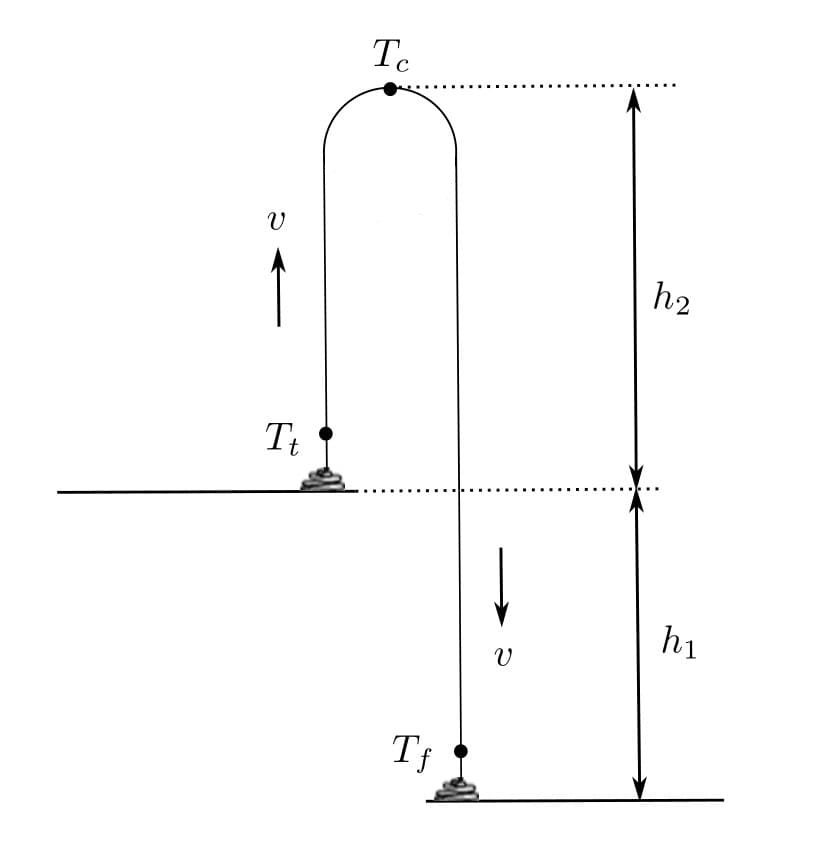
Мы готовы рассмотреть случай <<фонтана>>. Здесь и далее считаем, что <<фонтан>> уже установился и сохраняет постоянную форму и скорость, на столе и на полу лежат концы цепочки.

C1  ^0.20 По аналогии с пунктами B2 и B3 запишите выражения для сил натяжения цепи в разных точках: $T_t$ (над столом), $T_c$ (в петле вблизи потолка), $T_f$ (вблизи пола).

C2  ^0.40 Объединив записанные выражения с законом изменения импульса, решите систему уравнений и получите выражения для $v$ и для предполагаемой высоты <<фонтана>> $h_2$.

Поскольку полученный результат противоречит эксперименту, требуется скорректировать модель явления. Предположим, во-первых, что существует некая сила реакции опоры, действующая со стороны стола на <<подскакивающее>> со стола звено. Из соображений размерности эта сила должна быть пропорциональна $\lambda v^2$, поэтому пусть $R=\alpha \lambda v^2$, где $\alpha$ - некий численный коэффициент. Во-вторых, пусть натяжение цепи вблизи пола равно $\beta \lambda v^2$, где $\beta$ - также численный коэффициент.

C3  ^0.20 Чему равны коэффициенты $\alpha$ и $\beta$ в упрощенной модели, рассмотренной ранее в пункте C1?

C4  ^0.60 В описанных новых предположениях повторите выкладки, аналогичные пункту C2, и получите выражения для $\cfrac{h_2}{h_1}$ и для отношения $\cfrac{E_\text{кин}}{E_\text{пот}}$ кинетической энергии летящего звена к его начальной потенциальной энергии (отсчитываемой от уровня пола).

C5  ^0.60 Какому условию должны удовлетворять $\alpha$ и $\beta$, чтобы не нарушался закон сохранения энергии? При каких значениях $\alpha_0$ и $\beta_0$ достигается максимальная допустимая высота <<фонтана>>? Чему равны соответствующие этой оценке отношения $\left( \cfrac{h_2}{h_1} \right)_{max}$ и $\left( \cfrac{E_\text{кин}}{E_\text{пот}} \right) _{max}$?

Часть D. Эксперимент (0.2 балла)

Полученная оценка $h_2$ оказывается завышенной. На рисунке ниже приведён график $h_2(h_1)$, описывающий наблюдаемые в экспериментах величины эффекта.

D1  ^0.20 По графику рассчитайте экспериментальный коэффициент $\left( \cfrac{h_2}{h_1} \right)_{exp}$.

Часть E. Вращение звеньев (2.0 балла)

E1  ^1.10 Рассчитайте, какая сила $R$ должна подействовать на левый конец звена для возникновения такого движения. Ответ выразите через $m$, $b$, $I$, $\lambda$.

E2  ^0.30 Считая, что цепь - соединенные друг с другом <<штырьки>> (т.е. звенья - тонкие цилиндры), рассчитайте $\alpha_\text{шт.}$ - численное значение коэффициента, введенного ранее соотношением $R=\alpha \lambda v^2$. Примите $\beta \approx 0$ и найдите $\left( \cfrac{h_2}{h_1} \right)_\text{шт.}$.

E3  ^0.30 Считая теперь звенья тонкими обручами, рассчитайте $\alpha_\text{обр.}$. Примите $\beta \approx 0$ и найдите $\left( \cfrac{h_2}{h_1} \right)_\text{обр.}$.

E4  ^0.30 Рассчитайте $\alpha_3$. Примите $\beta \approx 0$ и найдите $\left( \cfrac{h_2}{h_1} \right)_3$.

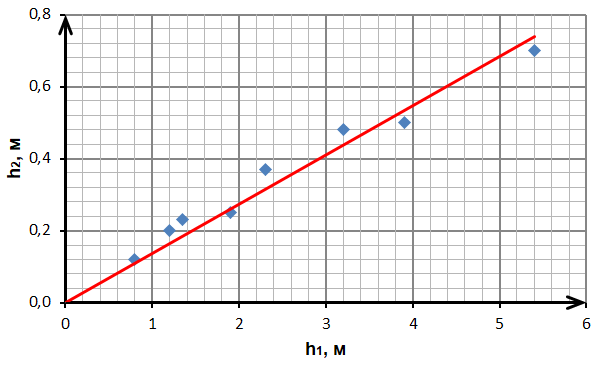
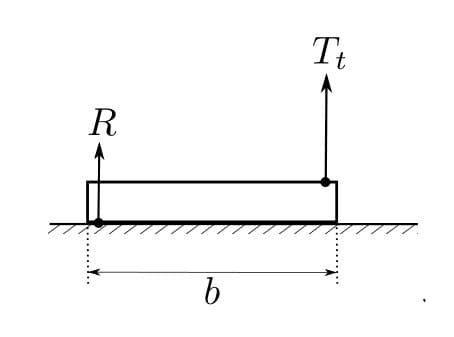
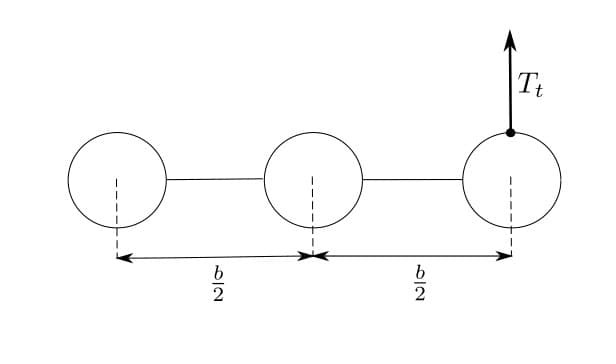
Помимо описанной причины возникновения $R$, связанной с неточечностью звеньев, есть еще много факторов, дающих вклад в эту силу, но их полноценный расчет сложен и сильно зависит от конструкции цепи. Например, если это бусы, то отрыв от стола может начинаться с горизонтального <<протаскивания>> нескольких бусинок по куче неподвижных. Во время такого <<протаскивания>> могут происходить удары, реакция опоры в которых будет иметь вертикальную составляющую. Дальнейший анализ процесса отрыва звеньев выходит за рамки задачи.

Часть F. Форма <<фонтана>> (2.5 балла)

В первую очередь рассмотрим задачу о <<цепной линии>>, т.е. опишем, какую форму принимает цепочка с закрепленными концами, статично висящая в поле тяжести. Пусть введена координата $s$, отсчитываемая вдоль цепочки от одного из ее концов. От $s$ зависят угол наклона $\theta(s)$ касательной к цепочке и сила натяжения $T(s)$. Рассмотрим маленькую дугу длины $ds$ в окрестности некоторого $s$.

F1  ^1.00 Записав второй закон Ньютона в проекции на касательную к цепочке и на перпендикуляр к ней, получите систему дифференциальных уравнений, связывающих функции $T(s)$, $\theta(s)$ и содержащих постоянные $\lambda$ и $g$. Решать систему не требуется.

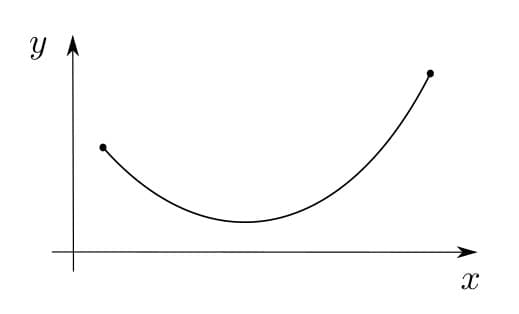
От <<статической>> задачи перейдем к <<динамической>>. Рассмотрим фонтанирующую цепочку и допустим, что форма <<фонтана>> установилась, т.е. траектории всех звеньев в точности повторяют друг друга. Скорость цепочки в <<фонтане>> равна $v$.

F2  ^1.00 Аналогично пункту F1, запишите систему дифференциальных уравнений, связывающих функции $T(s)$ и $\theta(s)$ для линии <<фонтана>>. Решать систему не требуется.

F3  ^0.50 Пусть $T (s)$ - натяжение в линии фонтана, т.е. функция, удовлетворяющая уравнениям из пункта F2. Функция $(T(s)-\tau)$ удовлетворяет системе уравнений для цепной линии из пункта F1 при некотором значении постоянной $\tau$. Выразите $\tau$.

Сила натяжения в каждой точке увеличена на $\tau$ по сравнению со <<статичной>> задачей, и это единственное отличие: известно, что подобная добавка к $T(s)$ не влияет на форму кривой. Таким образом, мы доказали, что <<фонтан>>  — тоже цепная линия!