Электрическая цепь, представленная на рисунке, состоит из трёх конденсаторов $C_1=C_2=C_3=C$, двух одинаковых резисторов $R_1=R_2=R$, источника постоянного напряжения $\mathcal{E}$ с нулевым внутренним сопротивлением и ключа $K$. Пока ключ был разомкнут, конденсаторы были не заряжены. Обозначим за $t$ время после замыкания ключа, заряды конденсаторов за $q_1$, $q_2$ и $q_3$ и силы тока в них ($I=dq/dt$) $I_1$, $I_2$ и $I_3$ в соответствии с их номерами.

A1  ^0.60 Найдите заряды конденсаторов $q_{1_0}$, $q_{2_0}$ и $q_{3_0}$ при $t\rightarrow0$.

A2  ^0.60 Найдите заряды конденсаторов $q_{1_{\infty}}$, $q_{2_{\infty}}$ и $q_{3_{\infty}}$ при $t\rightarrow\infty$.

A3  ^0.40 Найдите количество теплоты $Q_0$, выделившееся в системе за время $t\rightarrow0$.

A4  ^0.40 Найдите количество теплоты $Q_{\infty}$, выделившееся в системе за время $t\rightarrow\infty$.

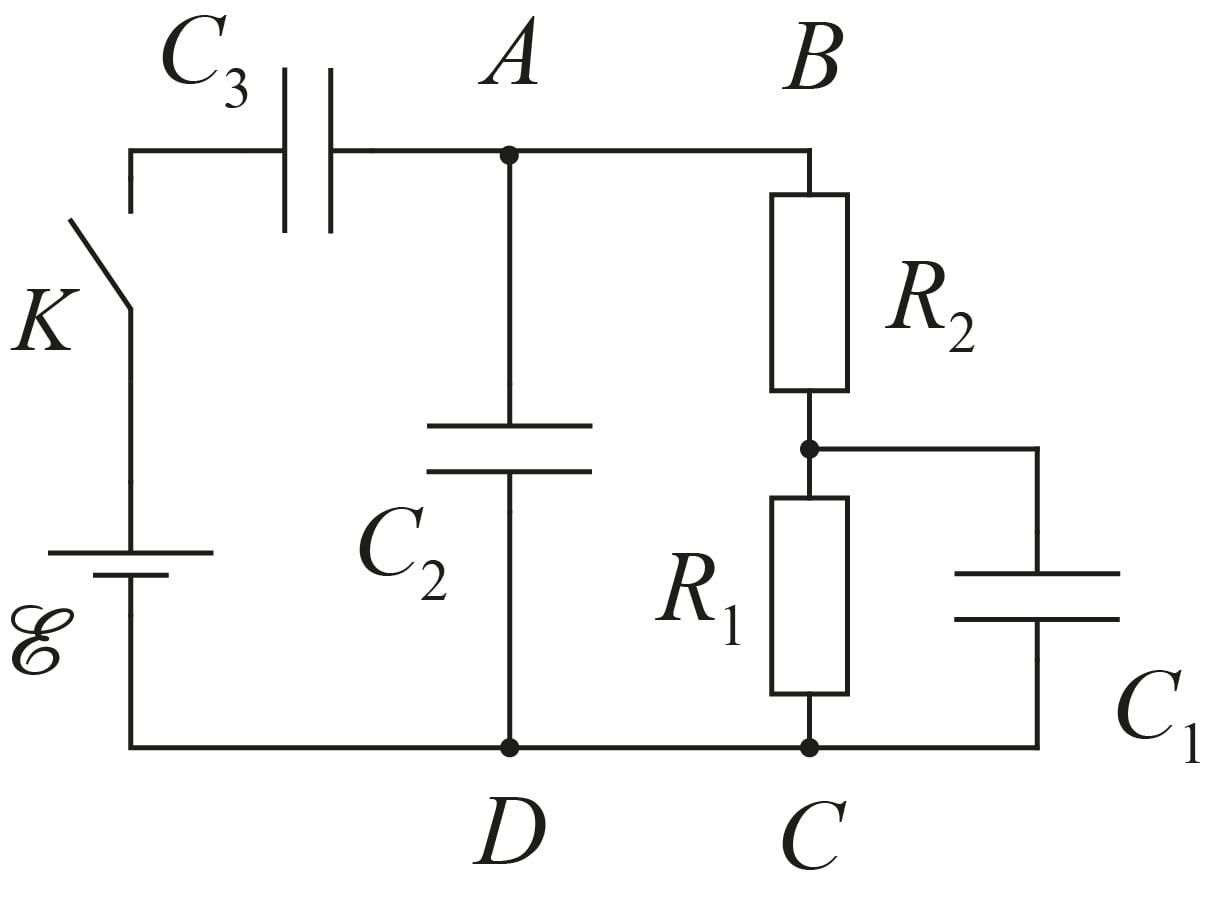
Перейдём к нахождению временной зависимости заряда первого конденсатора $q_1(t)$.

A5  ^0.50 Из первого закона Кирхгофа, записанного для узла $A$, выразите $I_2$ через $I_1$, $q_1$, $R$ и $C$.

A6  ^0.50 Из второго закона Кирхгофа, записанного для контура $ABCD$, выразите $q_2$ через $I_1$, $q_1$, $R$ и $C$. Найдите также $I_2$, дифференцируя $q_2$ по времени. Ответ выразите через $\cfrac{dI_1}{dt}$, $I_1$, $R$ и $C$.

A7  ^0.40 Приравнивая выражения для $I_2$, полученные в пунктах A5 и A6, покажите, что дифференциальное уравнение, описывающее зависимость $q_1(t)$ имеет следующий вид $$\alpha\frac{d^2q_1}{dt^2}+\beta\frac{dq_1}{dt}+q_1=0. $$ Выразите также $\alpha$ и $\beta$ через $R$ и $C$.

Далее считайте известным, что решение данного дифференциального уравнения нужно искать в виде $$q_1(t)=Ae^{\lambda{t}}, $$ где $\lambda$ зависит только от $R$ и $C$, а $A$ – от начальных условий.

A8  ^0.50 Найдите $\lambda_1$ и $\lambda_2$, удовлетворяющие уравнению, полученному в пункте A7. Ответы выразите через $R$ и $C$. В качестве $\lambda_1$ выберите большее из значений.

В действительности, зависимость $q_1(t)$ представляется в виде суммы найденных решений $$q_1(t)=A_1e^{\lambda_1{t}}+A_2e^{\lambda_2{t}} $$

A9  ^0.80 Из начальных условий найдите $A_1$ и $A_2$. Ответы выразите через $C$ и $\mathcal{E}$.

A10  ^1.30 Найдите количества теплоты $Q_{R_1}$ и $Q_{R_2}$, выделившиеся в резисторах за время $t\rightarrow\infty$. Ответы выразите через $C$ и $\mathcal{E}$.

$\textit{Примечание}$ : $\int e^{ax}dx=\frac{e^{ax}}{a}+C$