В 1973 году был предложен способ вывода спутников на гиперболическую орбиту с помощью гравитационного манёвра, который Вам предлагается проанализировать. В рамках данной задачи исследуется движение двух спутников 1 и 2, запущенных с противоположных полюсов Земли с одинаковыми по модулю и направлению скоростями $v$ по касательной к ней. Спутник 2 выводят на орбиту через малое время $\tau$ после запуска первого. Если на орбиту вывести только один из спутников, то его траектория будет представлять собой параболу. Масса спутника 1 равна $M_1$, а спутника 2 — $M_2\gg{M_1}$. Сопротивлением газа в атмосфере можно пренебречь, как и влиянием гравитационного притяжения со стороны других тел. Масса Земли $M_{\text{З}}\gg{M_2}$, радиус Земли — $R_{\text{З}}$, гравитационная постоянная — $G$. Обозначим за $P$ точку пересечения эллиптических орбит спутников, а за $\varphi$ - угол между направлениями их скоростей в данной точке. Движение спутника 1 состоит из трёх участков: 1) Движение по параболической орбите; 2) Взаимодействие со спутником 2 вблизи точки $P$; 3) Дальнейшее движение по гиперболической орбите в поле тяжести Земли.

Часть A. Траектория одного из спутников (3.3 балла)

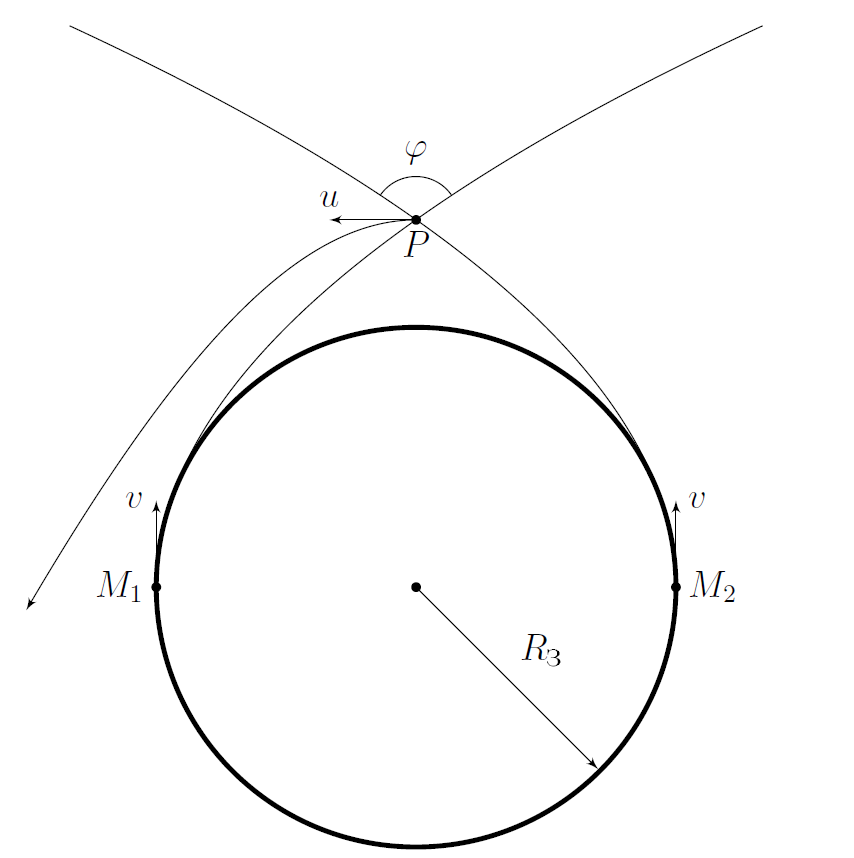
В данной части задачи вам предстоит приближённо описать траекторию спутников до точки пересечения $P$ их орбит.

A1  ^0.40 Чему равна скорость спутников $v$ в момент запуска? Ответ выразите через $G$, $М_З$ и $R_З$.

A2  ^0.60 На каком расстоянии от центра Земли $R_0$ находится точка $P$ пересечения траекторий спутников? Ответ выразите через $R_\text{З}$.

A3  ^0.80 Чему равен угол $\varphi$ между направлениями скоростей спутников в точке $P$?

A4  ^1.50 Найдите время $t_0$, через которое спутники достигают точки $P$. Ответ выразите через $G$, $R_\text{З}$ и $M_\text{З}$.

Здесь и далее считайте, что $\tau\ll{t_0}$. При приближении спутников к точке $P$ их взаимодействием с Землёй можно пренебречь.

Часть B. Взаимодействие спутников (4.0 балла)

B1  ^0.70 Считая, что вблизи точки $P$ спутники двигались вдоль прямых, направления которых совпадали с направлениями их скоростей в данной точке, найдите относительную скорость спутников $v_0$, а также минимальное расстояние $b$ между ними, пренебрегая их гравитационным взаимодействием. Ответ выразите через $v$ и $\tau$.

Далее считайте, что в системе отсчёта спутника 2 орбита спутника 1 представляет собой гиперболу с прицельным параметром $b$ на их бесконечно большом удалении. Также считайте, что на бесконечно большом удалении относительная скорость спутников равна $v_0$, найденной в предыдущем пункте.

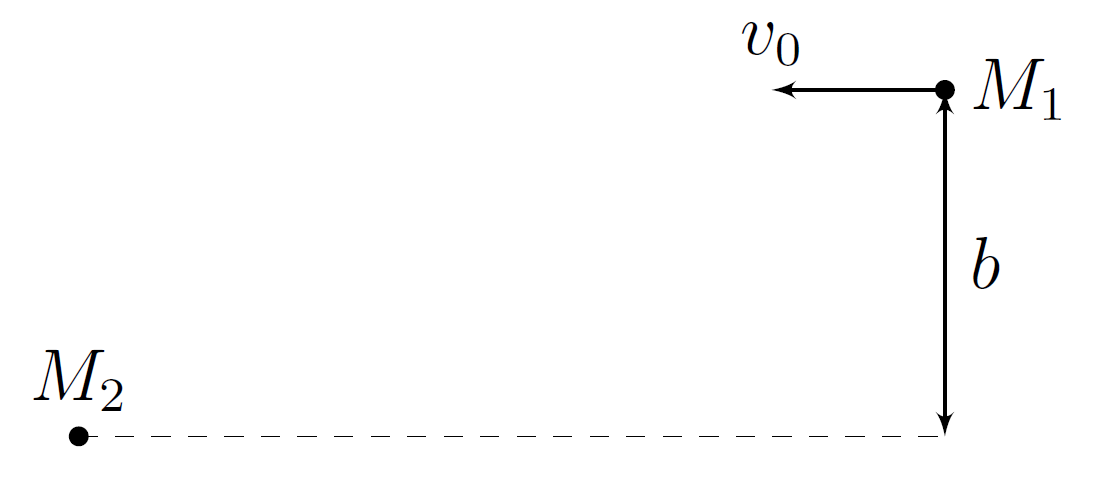
Когда взаимодействием спутников 1 и 2 вновь можно пренебречь, скорость спутника 1 в системе отсчёта Земли равна $u$ и направлена перпендикулярно линии, соединяющей его с Землёй.

B2  ^1.00 Найдите $u$. Ответ выразите через $v$.

B3  ^2.30 Найдите $\tau$. Ответ выразите через $G$, $M_2$, $M_3$ и $R_\text{З}$.

Часть C. Повторное движение в поле тяжести Земли (2.7 балла)

После взаимодействия со спутником 2 орбита спутника 1 в поле тяжести Земли представляет собой гиперболу.

C1  ^1.00 Найдите скорость $v_\infty$ спутника 1 на бесконечно большом удалении от Земли. Ответ выразите через $v$.

C2  ^1.50 Найдите угол $\varphi_\infty$ между векторами $\vec{u}$ и $\vec{v}_\infty$.

С3  ^0.20 Возможно ли действительно вывести спутник на орбиту таким образом? Ответ обоснуйте.