Электрическое поле внутри шара равняется нулю, а вне шара представляет собой сумму внешнего поля и поля диполя:
$$\vec{E}=\vec{E}_0+\cfrac{1}{4\pi\epsilon_0}\left(\cfrac{3\left(\vec{p}\cdot{\vec{r}}\right)\vec{r}}{r^5}-\cfrac{\vec{p}}{r^3}\right)
$$
На поверхности шара электрическое поле направлено перпендикулярно поверхности.
Отсюда:

По определению диполь представляет собой два точечных заряда $+q$ и $-q$, расположенные на расстоянии $l$ друг от друга.
Пусть $\vec{r}$ - радиус-вектор отрицательного заряда, а $\vec{l}$ - радиус-вектор положительного заряда относительно отрицательного.
Тогда для силы взаимодействия имеем:
$$\vec{F}=q\left(\vec{E}(\vec{r}+\vec{l})-\vec{E}(\vec{r})\right)
$$
Если электрическое поле направлено вдоль дипольного момента системы, то, поскольку диполь ориентирован вдоль оси $z$, сила, действующая на него, направлена вдоль оси $z$.
Если диполь можно считать точечным
$$E_z(\vec{r}+\vec{l})-E_z(\vec{r})=\cfrac{dE_z}{dz}\cdot{l}
$$
Отсюда для силы получим:
$$F_z=p_z\cfrac{dE_z}{dz}
$$
В нашей задаче поскольку $kR\ll{E_0}$ - модель электрического диполя хорошо описывает электрическое поле шара.
Подставляя выражение для $p_z$ и $\cfrac{dE_z}{dz}$, найдём:

Из теоремы Гаусса имеем:
$$2\pi rLE_\text{п}=\cfrac{q}{\epsilon_0}=\cfrac{\lambda L}{\epsilon_0}
$$
откуда:

При $r\gg{R}$ величины $E$ и $\cfrac{dE}{dr}$ поля провода на масштабах размеров шара могут считаться постоянными. В данном приближении дипольный момент шара равен:
$$p=\cfrac{2\lambda R^3}{r}
$$
Сила, действующая на шар, равна:
$$F_r=p\cfrac{dE_r}{dx}
$$
откуда:

Для потенциальной энергии имеем:
$$W_p=-\int\limits_r^{\infty}Fdr
$$
Интегрируя, находим:
$$W_p=-\cfrac{\lambda^2R^3}{2\pi\epsilon_0r^2}
$$
Отсюда параметр $A$ равен:

Из закона сохранения энергии имеем:
$$\cfrac{mv^2}{2}-\cfrac{A}{r^2}=\cfrac{mv^2_0}{2}
$$
Представим квадрат скорости в следующем виде:
$$v^2=\dot{r}^2+r^2\dot{\varphi}^2
$$
Из закона сохранения момент импульса получим:
$$L=mr^2\dot{\varphi}\Rightarrow{\dot{\varphi}=\cfrac{v_0b}{r^2}}
$$
Комбинируя с законом сохранения энергии, получим:
$$\cfrac{m\dot{r}^2}{2}+\cfrac{mv^2_0b^2}{2r^2}-\cfrac{A}{r^2}=\cfrac{mv^2_0}{2}
$$
Минимальное расстояние до провода достигается при $\dot{r}=0$. Отсюда получим:

Подкоренное выражение должно быть неотрицательным. Отсюда получим:

Явно продифференцируем $u$:
$$u'=\cfrac{du}{d\varphi}=-\cfrac{1}{r^2}\cfrac{dr}{d\varphi}
$$
Представим $\cfrac{dr}{d\varphi}$ как производную сложной функции:
$$\cfrac{dr}{d\varphi}=\cfrac{\dot{r}}{\dot{\varphi}}
$$
откуда:

Величина постоянна и равна:
$$r^2\dot{\varphi}=\cfrac{L}{m}=v_0b
$$
В начальный момент скорость направлена прямо на провод. Тогда находим:

Выражение для механической энергии шара следующее:
$$E=\cfrac{m\dot{r}^2}{2}+\cfrac{mr^2\dot{\varphi}^2}{2}-\cfrac{A}{r^2}
$$
Из закона сохранения момента импульса имеем:
$$L=mr^2\dot{\varphi}=mv_0b
$$
откуда:
$$E=\cfrac{m\dot{r}^2}{2}+\cfrac{mv^2_0b^2}{2r^2}-\cfrac{A}{r^2}
$$
Переходя к переменным $u$ и $u'$, получим:

Дифференцируя по $\varphi$ выражение для энергии, получим уравнение гармонических колебаний:
$$u''=-u\left(1-\cfrac{2A}{mv^2_0b^2}\right)
$$
с циклической частотой:
$$\omega_0=\sqrt{1-\cfrac{2A}{mv^2_0b^2}}
$$
Общее решение запишем в виде:
$$u(\varphi)=C\sin\left(\omega_0\varphi+\varphi_1\right)
$$
С учётом начальных условий:
$$u(0)=0\quad u'(0)=\cfrac{1}{b}
$$
Находим:

Величина $u$, начиная от нуля, достигает максимума, а затем, достигая нуля, остаётся постоянной во времени. График приведён на рисунке ниже:

Ответ:

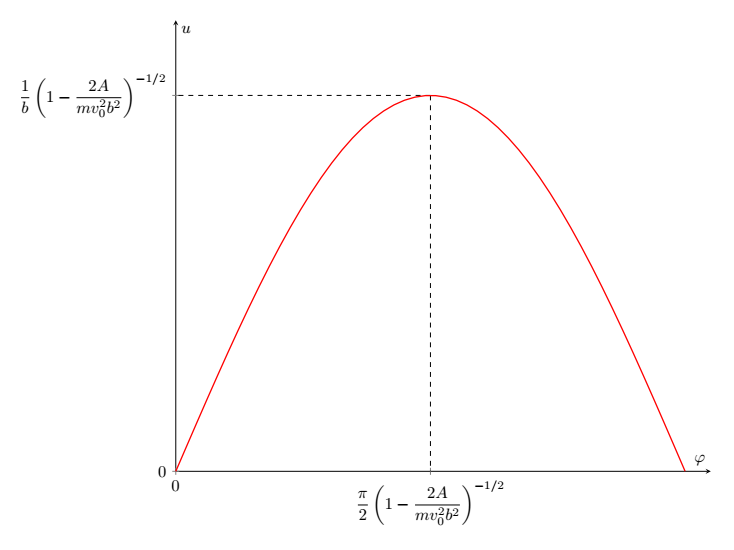
При изменении направления скорости шарика на противоположное, полное изменение угла $\varphi$ равно $2\pi$. Отсюда находим величину $\omega_0$:
$$\omega_0=\cfrac{1}{2}
$$
Тогда параметр $A$ равен:
$$A=\cfrac{3mv^2_1b^2}{8}
$$
Приравнивая с выражением, полученным в пункте $\textbf{A4}$
$$\cfrac{\lambda^2R^3}{2\pi\epsilon_0}=\cfrac{3mv^2_1b^2}{8}
$$
находим:

Введём в центре сферы цилиндрической систему координат с осью $z$, направленной вдоль линии, соединяющей центр сферы с зарядом $q_1$.
Потенциал зарядов $q_1$ и $-q_2$ в любой точке на поверхности шара равен нулю, поэтому:
$$\cfrac{q_1}{\sqrt{r^2+(x-L)^2}}=\cfrac{q_2}{\sqrt{r^2+(x-S)^2}}
$$
или:
$$(q^2_1-q^2_2)(r^2+x^2)+2x(q^2_2L-q^2_1S)+q^2_1S^2-q^2_2L^2=0
$$
Поскольку $r^2+x^2=R^2$, коэффициент при $x$ равен нулю. Тогда получим систему уравнений:
$$\cfrac{L}{S}=\cfrac{q^2_1}{q^2_2}\qquad (q^2_1-q^2_2)R^2=q^2_2L^2-q^2_1S^2
$$
решая которую, находим:

Для $dq_1$ имеем:
$$dq_1=\lambda rd\tan{\alpha}
$$
или:

Рассматриваемый элемент находится на расстоянии $L=\cfrac{r}{\cos\alpha}$ от центра шара. Отсюда найдём $dq_2$ и $S$:

Для $r_{-}$ имеем:
$$r_{-}=r-S\cos\alpha
$$
или

Пара зарядов-изображений притягивается к проводу, поскольку отрицательный заряд находится на меньшем расстоянии от провода.
Для силы притяжения с учётом электрического поля провода имеем:
$$dF=\cfrac{\lambda dq_2}{2\pi\epsilon_0}\left(\cfrac{1}{r_{-}}-\cfrac{1}{r}\right)
$$
или:

Для нахождения полной силы вычислим интеграл от выражения, полученного в пункте $\textbf{D3}$ в пределах от $-\cfrac{\pi}{2}$ до $\cfrac{\pi}{2}$.
Введём величину $t$, равную:
$$t=\cfrac{R\sin\alpha}{\sqrt{r^2-R^2}}
$$
Тогда получим:
$$F=\cfrac{\lambda^2R^2}{2\pi\epsilon_0r\sqrt{r^2-R^2}}\int\limits_{-\frac{R}{\sqrt{r^2-R^2}}}^{\frac{R}{\sqrt{r^2-R^2}}}\cfrac{dt}{1+t^2}=\cfrac{\lambda^2}{\pi\epsilon_0}\cfrac{R}{r}\cfrac{R}{\sqrt{r^2-R^2}}\arctan\cfrac{R}{\sqrt{r^2-R^2}}
$$
Учитывая связь $r$, $R$ и $\theta$, находим:

Учитывая, что шар притягивается к проводу, выражение для потенциальной энергии следующее:
$$W_p=-\int\limits_r^{\infty}F(r)dr
$$
Найдём величину $dr$ в переменных $R$ и $\theta$:
$$dr=d\left(\cfrac{R}{\sin\theta}\right)=-\cfrac{R\cos\theta d\theta}{\sin^2\theta}
$$
Тогда имеем:
$$W_p=-\cfrac{\lambda^2R}{\pi\epsilon_0}\int\limits_0^{\theta}\theta d\theta
$$
откуда:

В момент контакта шара и провода $\theta=\cfrac{\pi}{2}$.
Запишем закон сохранения энергии:
$$\cfrac{mv^2_0}{2}=\cfrac{\lambda^2R}{2\pi\epsilon_0}\left(\cfrac{\pi}{2}\right)^2
$$
откуда:

Из закона сохранения энергии имеем:
$$\cfrac{mv^2}{2}-\cfrac{\lambda^2R\theta^2}{2\pi\epsilon_0}=\cfrac{mv^2_0}{2}
$$
Представим скорость в следующем виде:
$$v^2=\dot{r}^2+r^2\dot{\varphi}^2
$$
С учётом закона сохранения момента импульса
$$L=mv_0b=mr^2\dot{\varphi}
$$
находим:

В зависимости от величины $v_0$ функции делятся на три типа:
1) пересекающие ось ординат при $\theta<\cfrac{\pi}{2}$;
2) не пересекающие ось ось ординат;
3) касающиеся оси ординат при $\theta<\cfrac{\pi}{2}$.

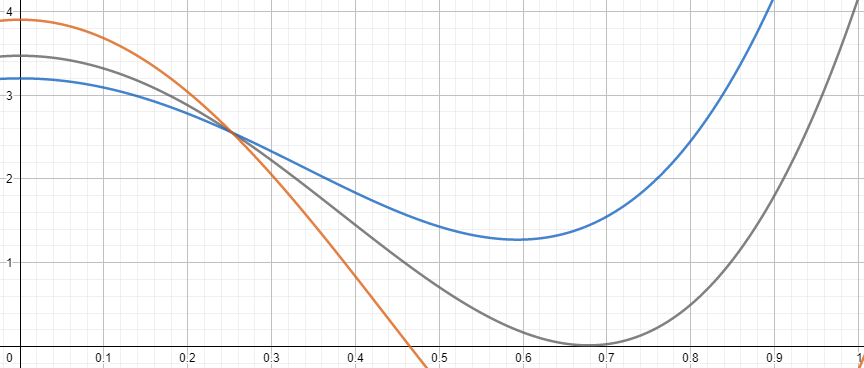
При достаточно больших скоростях (функция 1-го типа) график пересекает ось ординат. В момент пересечения величина $\dot{r}$ изменяется на противоположную, поскольку $\dot{r}^2>0$.
При достаточно низких скоростях (функция 2-го типа) значение $\dot{r}^2$ в экстремуме положительно, поэтому шар падает на провод.
Функция 3-го типа является граничным случаем рассмотренных выше - в экстремуме значение функции $\dot{r}^2$ обращается в ноль.
При сколь угодно больших скоростях шар не коснётся провода.
Отсюда ясно, что в равенства нулю величины $\dot{r}^2$ нужно также приравнять нулю производную $\cfrac{d\dot{r}^2}{d\varphi}$, что в виде системы записывается следующим образом:

Из уравнения для равной нулю производной находим:
$$v_0=\lambda\sqrt{\cfrac{R}{\pi\epsilon_0m}}\cdot{\cfrac{R}{b}\sqrt{\cfrac{2\theta_{max}}{\sin2\theta_{max}}}}
$$
Для нахождения $v_0$ необходимо определить $\theta_{max}$.
Разделив уравнения друг на друга, получим:
$$\cfrac{k^2\sin^2\theta_{max}-1}{k^2\sin2\theta_{max}}=\cfrac{\theta_{max}}{2}\quad k=\cfrac{b}{R}
$$
Решая уравнение на калькуляторе, находим:
$$\theta_{max1}=0{,}296~\text{рад}\quad\theta_{max2}=0{,}793~\text{рад}\quad\theta_{max3}=1{,}459~\text{рад}
$$
откуда: