Пусть $\vec{E}$ — напряженность электрического поля, $\vec{H}$ — напряженность магнитного поля, $\vec{D}$ — электрическая индукция, $\vec{B}$ — индукция магнитного поля. Известно, что $\vec{D}=\epsilon_0\vec{E}+\vec{P}$, где $\vec{P}$ — вектор поляризации вещества, $\epsilon_0$ — электрическая постоянная. Будем рассматривать только немагнитные вещества, для них $\vec{B}=\mu_0 \vec{H}$, где $\mu_0$ — магнитная постоянная. Плотность энергии электромагнитного поля вычисляется по формуле $u_{em}=\frac{1}{2}(\vec{E}\cdot\vec{D}+\vec{H}\cdot\vec{B})$, плотность потока энергии (вектор Пойнтинга) $\vec{S}=\vec{E}\times \vec{H}$.

Плоская монохроматическая световая волна в однородной среде задаётся величинами: угловая частота $\omega$, волновой вектор $\vec{k}$, $\vec{D}$, $\vec{B}$. Из уравнений Максвелла: $\vec{k}\times\vec{E}=\omega \vec{B}$ и $\vec{k}\times\vec{H}=-\omega \vec{D}$. В такой волне векторы $\vec{D}$ и $\vec{B}$ меняются в пространстве и во времени по синусоиде с фазой $(\vec{k} \cdot \vec{r} -\omega t)$.

Часть A. Распространение света в изотропном диэлектрике (1.0 балл)

В изотропной среде $\vec{P}=\chi \epsilon_0 \vec{E}$ и $\vec{D}=\epsilon \vec{E}$, где $\chi$ — магнитная восприимчивость, $\epsilon = \epsilon_0 (1+\chi)$ — магнитная проницаемость. Фазовая скорость волны равна $v_p = c/n$, где $c$ — скорость света в вакууме, $n\:$— показатель преломления. Можно также представлять свет набором лучей, направленных вдоль переноса энергии и имеющих скорость $v_r$, с которой переносится плотность энергии.

Рассмотрим плоскую световую волну с угловой частотой $\omega$ и волновым вектором $\vec{k}$ в однородной изотропной диэлектрической среде.

A1  ^0.40 Получите выражение для фазовой скорости $v_p$ через $\epsilon$ и $\mu_0$.

A2  ^0.20 Напишите, как выражается показатель преломления $n$.

A3  ^0.40 В каком направлении $\hat{S} \equiv \vec{S}/S$ переносится энергия? Какова скорость лучей $v_r$?

Часть B. Распространение света в одноосной среде (4.8 балла)

Теперь предположим, что среда имеет выделенное направление $z$ ({\it оптическую ось}): $D_x = \epsilon E_x$, $D_y = \epsilon E_y$, $D_z = \epsilon' E_z$, где все оси попарно ортогональны. Тогда фазовая скорость зависит еще и от направлений $\vec{k}$ и $\vec{D}$. Обозначив $n_o = c \sqrt{\mu_0 \epsilon}$ и $n_e=c \sqrt{\mu_0 \epsilon'}$, выполните пункты {\bf B.1}, {\bf B.2}, и {\bf B.3}.

B1  ^1.50 Пусть волновой вектор $\vec{k}$ лежит в плоскости $xz$: $\vec{k}=k(\sin \theta,0,\cos \theta)$. При заданном $\theta$ плоская монохроматическая волна может распространяться только при определенных направлениях $\vec{D}$ и $\vec{B}$.

Найдите эти возможные направления.

Выразите также все соответствующие показатели преломления через $\theta$, $n_o$ и $n_e$.

При каком угле $\theta$ возможно лишь одно значение показателя преломления?

B2  ^0.80 Поляризация световой волны (направление колебаний $\vec{E}$) может быть перпендикулярна плоскости $xz$ ({\it обыкновенная волна}, {\it обыкновенный луч}) или лежать в этой плоскости ({\it обыкновенная волна/луч}).

Для каждой из волн, найденных вами в {\bf B.1}, запишите единичный вектор в направлении поляризации.

Укажите, какая из них обыкновенная, а какая — необыкновенная.

Вычислите $\tan \alpha$, где $\alpha$ — угол между $\vec{E}$ и $\vec{D}$ ($\alpha$ положительный, если вектора $\vec{E}$ и $\vec{D}$ лежат в плоскости $xz$ и поворот от $\vec{E}$ к $\vec{D}$ происходит по часовой стрелке).

B3  ^0.60 Используйте результаты пунктов {\bf B.1} и {\bf B.2} в случае, когда $\vec{k}$ по-прежнему составляет угол $\theta$ с положительным направлением оси $z$, но не лежит в плоскости $xz$.

Укажите возможные значения показателя преломления и соответствующие поляризации.

В одноосных средах направление светового луча может отличаться от направления вектора $\vec{k}$. Фазовая скорость по-прежнему вычисляется как $c/n$ ($n$ соответствует направлению $\vec{k}$). А скорость лучей определяется с учетом направления и плотности потока энергии.

B4  ^0.80 Пусть $\vec{k} = k(\sin \theta,0,\cos \theta)$, как в пунктах {\bf B.1-3}. Угол между $\hat{k} \equiv \vec{k}/k$ и направлением луча, $\hat{S}$, обозначим $\alpha_r$ ($\alpha_r$ положительный, если вектора $\hat{S}$ и $\hat{k}$ лежат в плоскости $xz$ и поворот от $\hat{S}$ к $\hat{k}$ происходит по часовой стрелке).

Найдите возможные значения $\tan \alpha_r$, скорости лучей $v_r$ и вектора Пойнтинга $\hat{S}$. Используя эти результаты, выразите величину $n_s = c/v_r$ через $\hat{S}$, $\hat{x}$, $\hat{z}$, $n_o$, $n_e$.

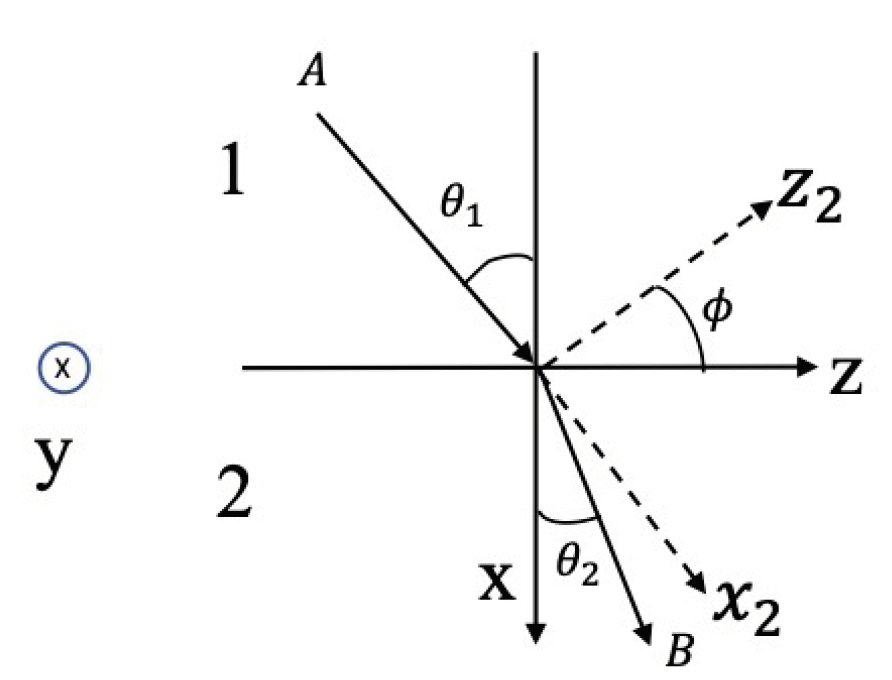
Пусть луч света идет из A в B через границу раздела изотропной (1) и анизотропной (2) сред (см. рис. 1). Плоскость $yz$ — граница раздела, $xz$ — плоскость падения, и в ней же лежит направление поляризации. Угол падения $\theta_1$. Показатель преломления (1) равен $n$, показатели преломления (2) для направлений $z_2$, $y_2$, $x_2$ равны $n_e$, $n_o$, $n_o$ соответственно. Причем ось $y_2$ совпадает с осью $y$. Из принципа Ферма следует:

$$\bar{A} (\tan \theta_2 )^2 + \bar{B} \tan \theta_2 +\bar{C}=0$$

B5  ^1.10 Получите выражения для $\bar{A}$, $\bar{B}$, $\bar{C}$ через $P_1$, $P_2$, $P_3$ и $n \sin \theta_1$, где $P_1=n^2_o \cos^2 \phi+n^2_e \sin^2 \phi$, $P_2=n^2_o \sin^2 \phi+n^2_e \cos^2 \phi$, $P_3=(n^2_o - n^2_e) \sin \phi \cos \phi$. С помощью уравнения (1) найдите $\tan \theta_2$ для двух случаев ориентации: $\phi =0$ и $\phi = \pi/2$.

Часть C. Запутанность света (4.2 балла)

В нелинейной среде напряженность электрического поля $\vec{E}$ связана с вектором поляризации $\vec{P}$ выражением $P_i=(\epsilon-\epsilon_0)E_i + \sum_j \sum_k \chi^{(2)}_{ijk} E_jE_k$. Здесь $i$, $j$, $k$ каждый может быть любым из трёх компонент $x$, $y$, $z$. $\chi^{(2)}_{ijk}$ есть константы, представляющие нелинейную восприимчивость среды второго порядка. Ненулевые $\chi^{(2)}_{ijk}$ приводят к тому, что при прохождении через нелинейную среду световая волна может расщепиться на две световые волны.

Предположим, что поскольку не все $\chi^{(2)}_{ijk}$ равны нулю, электрическое поле в среде является суперпозицией трёх плоских волн с угловыми частотами $\omega$, $\omega_1$, и $\omega_2$, распространяющиеся с волновыми векторами $\vec{k}$, $\vec{k}_1$, и $\vec{k}_2$, соответственно. Будем считать, что $\omega \geq \omega_2$ и $\omega_1 \geq \omega_2$.

C1  ^0.80 Найдите все возможные отношения (известные как {\it условия фазового синхронизма}) между этими угловыми частотами и волновыми векторами.

Если рассматривать свет состоящим из фотонов, какие законы сохранения подразумевают эти условия для трех указанных фотонов?

Запишите уравнения, выражающие эти законы сохранения для случая, когда фотон с угловой частотой $\omega$ и волновым вектором $\vec{k}$ расщепляется на два фотона с угловыми частотами $\omega_1$и $\omega_2$, распространяясь с волновыми векторами $\vec{k}_1$и $\vec{k}_2$, соответственно.

C2  ^0.80 Рассмотрим световую волну в одноосной среде. Обозначим обыкновенный луч как ${\bf o}$ и необыкновенный луч как ${\bf e}$. Есть 8 возможных путей расщепления световой волны: ${\bf o → o + o}$, ${\bf o → e + o}$, ${\bf o → o + e}$, ${\bf o → e + e}$, ${\bf e → o + o}$, ${\bf e → e + o}$, ${\bf e → o + e}$, и ${\bf e → e + e}$. Предположим, что коэффициенты преломления $n_o$ и $n_e$ оба являются возрастающей функцией от $\omega$. Используя те же обозначения как и в вопросе C1 и считая что $\vec{k}$, $\vec{k}_1$, и $\vec{k}_2$ коллинеарны, укажите какие из 8 путей расщепления не могут быть возможны.

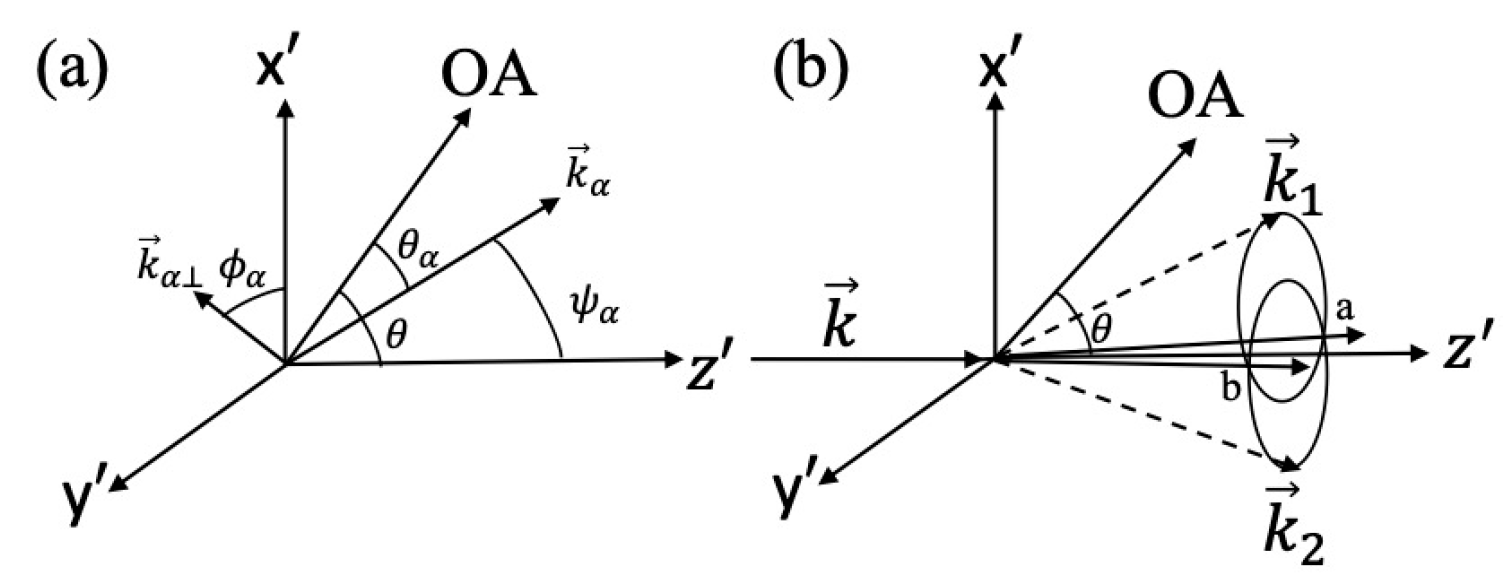
Рассмотрим падающий ${\bf e}$ луч распространяющийся вдоль направления оси $z'$ с волновыми вектором $\vec{k}$ и $\omega=\Omega_p$ в одноосной среде с показателем преломления $n_e < n_o$. Предположим, что при коллинеарном расщеплении ${\bf e → e + o}$, условие фазового синхронизма выполняется для $k_1=K_e$, $\omega_1=\Omega_e$, $k_2=K_o$, и $\omega_2=\Omega_o$. Здесь индексы 1 и 2 относятся к ${\bf e}$ лучу и к ${\bf o}$ лучу. Векторы $\vec{k}_1$, $\vec{k}_2$ и $\vec{k}$ все сонаправлены с направлением $z'$. Как показано на рис. 2(a), оптическая ось (the optic axis, OA) среды лежит в плоскости $x'z'$ и имеет угол $\theta < \pi/2$ с осью $z'$. Поэтому, получается что $n_e$ есть функция от $\omega$ и $\theta$, т.е., $n_e=n_e(\omega,\theta)$. Для того же падающего луча ${\bf e}$ с волновым вектором $\vec{k}$ и $\omega=\Omega_p$, предположим неколлинеарное расщепление лучей ${\bf e + o}$. Такое расщепление двух последних указанных лучей приводит к тому, что они расщепляются но остаются на двух конусах с $\omega_1=\omega_2=\Omega$, $k_1=k_2$, как показано на рис. 2(b). Отметим, что при коллинеарном расщеплении, $\Omega_e$ уже близко к $\Omega_o$, и здесь $\Omega$ лишь немного меньше $\Omega_e$. В плоскости перпендикулярной к $\vec{k}$, два круговых сечения конусов $\vec{k}_1$ и $\vec{k}_2$ пересекаются в точках $a$ и $b$ так, что линия $\overline{ab}$ параллельна оси $y'$. Как показано на рис. 2(a), $\vec{k}_{\alpha}$($\alpha=1,2$ ) составляет угол $\theta_{\alpha}$ с оптической осью и имеет угловые координаты $(\psi_{\alpha}, \phi_{\alpha})$. Здесь $\vec{k}_{\alpha \perp}$ является проекцией на плоскость $x'y'$. Каждый вектор $\vec{k}_{\alpha}$ отклоняется от оси $z'$только на малую величину $|(\Omega-\Omega_e)/\Omega_e| \ll 1$, $|\vec{k}_{\alpha \perp}|/k_{\alpha} \ll 1$ и $|\theta_{\alpha}-\theta| \ll 1$. Используя приближение, которые согласуются с $z'$ компонентой $\vec{k}_{\alpha}$ до членов порядка $k^2_{\alpha \perp}$ и угол $\theta_{\alpha}$ до $(\theta_{\alpha}-\theta)^2$, можно показать что $\vec{k}_{2\perp}=(q_{x'},q_{y'})$ удовлетворяет выражению $M (q_{x'}+ N )^2+M q^2_{y'}= L$.

C3  ^1.30 Пусть $M >0$. Выразите $M$, $N$, и $L$ через $\Omega$, $\Omega_e$, $\Omega_o$, $K_e$, $K_o$ и $N_e (\omega,\theta)=\frac{1}{n_e(\omega,\theta)}\frac{dn_e(\omega,\theta)}{d \theta}$ и групповые скорости $u_o=\frac{dw_2}{d k_2}$ и $u_e =\frac{d \omega_1}{d k_1}$ для ${\bf o}$ и ${\bf e}$ лучей. Оцените угол между осью конуса и осью $z'$, и также оцените угол между осью и образующей конуса через $L$, $M$, $N$ and $K_o$.

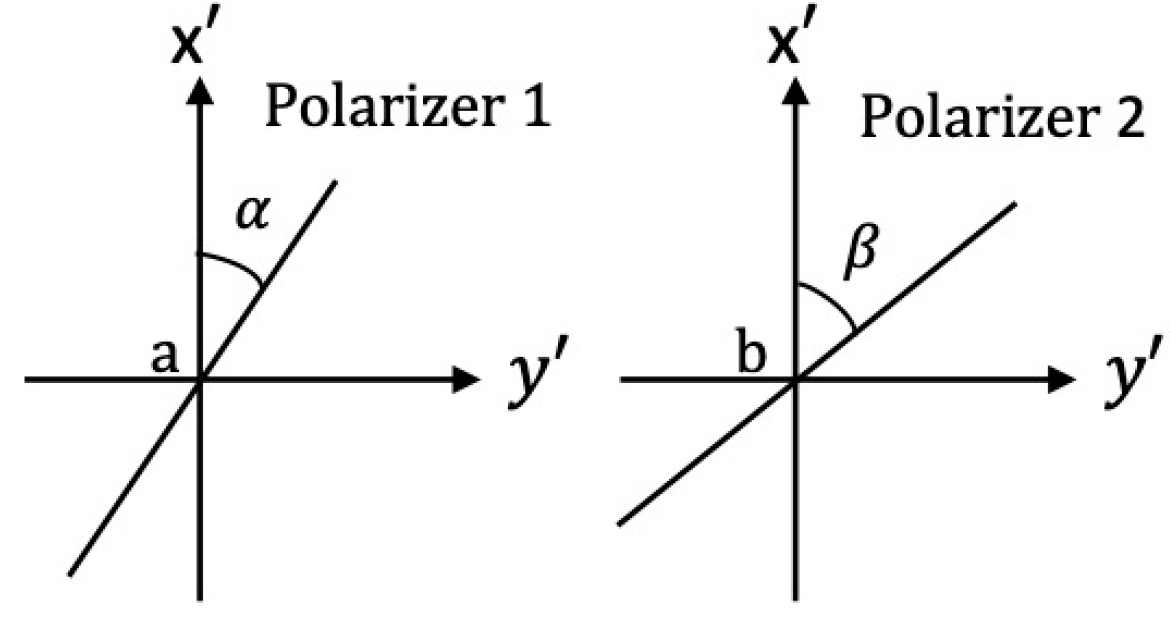
Вопрос C3 показывает, что фотон может разделиться на два фотона, которые при прохождении через точки a и b поляризованы в перпендикулярных направлениях. Эти два фотона называются ${\it запутанной~парой~фотонов}$, потому что если один фотон, проходящий через $a$ (называемый $a$-фотоном), поляризован в направлении $\hat{x}'$, то другой, который проходит через $b$ (называемый $b$-фотоном), будет поляризован в направлении $\hat{y}' \perp \hat{x}'$, и если $a$-фотон поляризован в $\hat{y}'$, то $b$-фотон будет поляризован в $\hat{x}'$. Запутанное состояние пары фотонов может быть получено экспериментально. Это суперпозиция двух вышеуказанных альтернативных состояний и может быть выражена как $\frac{1}{\sqrt{2}} (|\hat{x}'_a \rangle|\hat{y}'_b\rangle+|\hat{y}'_a \rangle|\hat{x}'_b\rangle)$. Здесь $|\hat{x}'_a \rangle|\hat{y}'_b\rangle $представляет состояние когда $a$-фоторн поляризован в направлении $\hat{x}'$ и $b$-фотон поляризован в направлении $\hat{y}'$; аналогичное значение имеет $|\hat{y}'_a \rangle|\hat{x}'_b\rangle $. Коэффициент $1/\sqrt{2}$ может рассматриваться как произведение амплитуд электрического поля (выраженное в соответсвующих единицах) для $a$- и $b$-фотонов. Как показано на рис. 3, два линейных поляризатора 1 и 2 имеют оси пропускания под углами $\alpha$ и $\beta$ соответственно относительно $\hat{x}'$. Мы можем использовать их для измерения совпадений двух фотонов, прошедших через $a$ и $b$. Пусть вероятность одновременного обнаружения двух фотонов, проходящих через поляризаторы 1 и 2, равна $P(\alpha,\beta)$. Другими словами, $P(\alpha,\beta)$ можно также рассматривать как величину, пропорциональную произведению интенсивностей (после соответствующих суперпозиций) света, проходящего через два поляризатора. Обозначим $\alpha+\pi/2$ и $\beta+\pi/2$ как $\alpha_{\perp}$ и $\beta_{\perp}$ соответственно.

C4  ^0.80 Рассмотрим полное электрическое поле, создаваемое линейными поляризаторами. Найдите вероятности $P(\alpha,\beta)$, $P(\alpha,\beta_{\perp})$, $P(\alpha_{\perp},\beta)$, и $P(\alpha_{\perp},\beta_{\perp})$.

C5  ^0.50 Обозначим $\sigma_a=1$ когда поляризатор 1 с углом $\alpha$ находит $a$-фотон и $\sigma_a=-1$ когда поляризатор 1 с углом $\alpha_{\perp}$ находит $a$-фотон. Аналогично, $\sigma_{\beta}=1$ или $-1$ обозначают случаи когда поляризатор 2 с углами $\beta$ или $\beta_{\perp}$ находят $b$-фотон.

Если $E(\alpha,\beta)$ обозначает среднее от $\sigma_a \sigma_b$, то величина $S=|E(\alpha,\beta)-E(\alpha,\beta')|+|E(\alpha',\beta)-E(\alpha',\beta')|$ имеет чрезвычайно важное значение. Для классической теории света $S \leq 2$. Это одна из формулировок неравенства Белла (CHSH-неравенства, полученного Клаузером, Хорном, Шимони и Хольтом).

Получите выражение для $S$ и вычислите $S$ для случая $\alpha=\frac{\pi}{4}$,$\alpha'=0$ , $\beta=-\frac{\pi}{8}$, $\beta'=\frac{\pi}{8}$.

Укажите, согласуется ли результат для $S$ с классической теорией.