Поверхностно-усиленная рамановская спектроскопия (SERS) – одно из самых ярких оптических явлений из открытых за последние 40 лет. В основе SERS лежит плазмонный резонанс – сильное увеличение электрического поля вблизи металлических наногранул при определенных условиях. Чтобы определить эти условия и понять, как работает SERS, необходимо научиться описывать свойства металла, помещенного в переменное электромагнитное поле.

Напомним, что свойства вещества в электрическом поле подчиняются следующим соотношениям:
$$\vec{D}=\varepsilon_0\varepsilon\vec{E}\quad\vec{D}=\varepsilon_0\vec{E}+\vec{P}
$$
где $\vec{E}$ и $\vec{D}$ — напряженность и индукция электрического поля соответственно, $\varepsilon$ — диэлектрическая проницаемость вещества, $\vec{P}$ — вектор поляризации (дипольный момент единицы объема), $\varepsilon_0=8{,}85\cdot{10^{-12}} \text{Ф}/\text{м}$ — электрическая постоянная.
На границе раздела двух сред в отсутствии свободных зарядов непрерывны касательная компонента вектора напряженности и нормальная компонента вектора индукции электрического поля.
В случае переменного электрического поля диэлектрическая проницаемость вещества (в том числе металлов) зависит от частоты электромагнитного поля.

Часть A. Газ свободных электронов

Рассмотрим бесконечное пространство, заполненное металлом: положительно заряженные ионы образуют регулярную кристаллическую решетку, в пространстве между ними движутся свободные электроны, концентрации зарядов обоих знаков одинаковы и равны $n$.

Внутри металла создано однородное переменное электрическое поле $\vec{E}\sin\omega t$. Ионы бесконечно тяжелые и неподвижные, а эффективныe массы электронов равны $m$. В рамках простейшей модели можно считать, что действующее на отдельный электрон поле совпадает с $\vec{E}\sin\omega t$. Все остальные силы (в том числе диссипативные) малы.

A1  ^1.10 Электрическое поле приводит к согласованному смещению $\vec{r}(t)$ электронов в направлении поля. Определите зависимость $\vec r(t)$ и вектор поляризации среды $\vec P(t)$ в установившемся режиме.

A2  ^0.30 Вычислите диэлектрическую проницаемость металла $\varepsilon(\omega)$ и постройте график этой зависимости.

Часть B. Плазмонный резонанс

B1  ^2.60 Определите поле $\vec{E}_{in}$ внутри шара и его дипольный момент $\vec{d}_0$ .

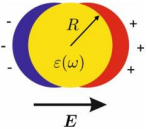
Изучим поведение металлического шара радиуса $R$ в поле плоской волны с частотой $\omega$ и амплитудой $\vec{E}_0$. Оказывается, если длина волны и глубина проникновения поля в металл намного превосходят размер шара, то его поведение аналогично поведению диэлектрического шара в постоянном электрическом поле, только в качестве диэлектрической проницаемости нужно брать величину $\varepsilon(\omega)$, аналогичную вычисленной в предыдущем пункте. По мере прохождения волны амплитуда внешнего поля в месте нахождения шара изменяется $\vec{E}=\vec{E}_0\cos\omega t$, а дипольный момент также изменяется $\vec{d}=\vec{d}_0\cos\omega t$.

B2  ^0.70 Нарисуйте картину силовых линий электрического поля в системе (внутри, вблизи и вдали от шара), считая $\varepsilon(\omega)=-3$.

B3  ^0.20 При некотором значении $\varepsilon(\omega_{res})=\varepsilon_{res}$ амплитуда электрического поля внутри шара $\left|\vec{E}_{in}\right|$ начинает неограниченно возрастать. Определите значение $\varepsilon_{res}$.

Значительное возрастание амплитуды электрического поля внутри и снаружи шара при частоте $\omega_{res}$ называется плазмонным резонансом. Мы получили бесконечный ответ, поскольку не учитывали диссипацию энергии. Теперь учтем диссипацию и будем считать, что основные потери в системе связаны с дипольным излучением.

B4  ^0.60 Осциллирующий диполь излучает энергию. Оцените мощность $I$ этих потерь, используя анализ размерностей и тот факт, что интенсивность дипольного излучения зависит только от амплитуды дипольного момента $\left|\vec{d}_0\right|$, частоты его колебаний $\omega_{res}$, скорости распространения волн c и электрической постоянной $\varepsilon_0$.

B5  ^3.80 Оцените среднюю энергию, вкачиваемую в систему за счет внешнего поля в условиях плазмонного резонанса при $\omega=\omega_{res}$. Из условия баланса энергии оцените амплитуду поля внутри шара в резонансе.

Часть C. Рамановская спектроскопия

Перейдем ко второй части задачи и рассмотрим рамановское рассеяние, которое также лежит в основе SERS. Разговор начнем с обсуждения устройства молекул. Будем представлять молекулу как множество грузиков (атомов), соединенных друг с другом пружинками (химическими связями). Для простоты мы в дальнейшем рассматриваем молекулу, состоящую всего из двух атомов.

C1  ^0.70 Рассмотрим два грузика с массами $m_1$ и $m_2$, соединенные между собой пружиной с жесткостью $k$. Определите частоту $\omega_0$ малых колебаний в системе.

Сложная молекула будет характеризоваться не одной частотой $\omega_0$, а целым спектром собственных частот. Знание этого спектра позволяет однозначно идентифицировать вещество, с которым мы имеем дело. В этом и заключается основная идея SERS.
Изучим поведение молекулы во внешнем электрическом поле $\vec{E}_0\cos\omega t$. Для простоты будем считать, что атомы не заряжены, т.е. в отсутствие внешнего поля молекула не обладает дипольным моментом. Однако во внешнем поле, подобно металлическому шарику, молекула поляризуется, т.е. приобретает дипольный момент
$$\vec{d}=\varepsilon_0\alpha\vec{E}_0\cos\omega t
$$
где $\alpha$ – поляризуемость молекулы. Здесь мы считаем, что направление индуцированного дипольного момента $\vec{d}$ совпадает с направлением внешнего поля

C2  ^0.20 Считая малой амплитуду механических колебаний около положения равновесия, напишите явное выражение для $\alpha(x)$ в линейном приближении, если $\alpha(0)=\alpha_0$ и $\frac{d\alpha}{dx}\bigg|_{x=0}=\beta_0$.

C3  ^0.20 Вычислите дипольный момент двухатомной молекулы во внешнем поле $\vec{E}_0\cos\omega t$. Ответ представьте в виде:
$$\vec{d}=\sum_i\vec{d}_i\cos\omega_it
$$

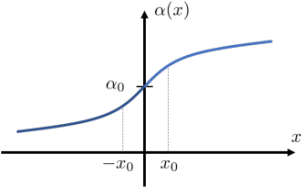
C4  ^0.20 Детектор регистрирует дипольное излучение молекулы. Выражению из предыдущего пункта будут соответствовать несколько пиков на частотах $\omega_i$. Высота каждого пика равна интенсивности излучения отдельного диполя $\vec{d}_i$ . Для каждого пика определите его частоту и высоту. Выразите ответ через $\varepsilon_0$, $\alpha_0$, $\beta_0$, $x_0$, $\omega$, $\omega_0$ и $\vec{E}_0$.

Наличие пиков на частотах отличных от $\omega$ называется рамановским рассеянием. Чтобы на детектор поступил хороший сигнал, необходимо поместить молекулу в сильное электрическое поле. Это сильное поле можно создать с помощью плазмонного резонанса. В этом и состоит основное отличие идеи SERS от обычной рамановской спектроскопии.

Часть D. Поверхностно-усиленная рамановская спектроскопия

Рассмотрим шар с диэлектрической проницаемостью $\varepsilon(\omega)$ в однородном переменном поле амплитуды $\left|\vec{E}_0\right|$ в условиях плазмонного резонанса.

D1  ^1.20 В какую точку пространства нужно поместить молекулу исследуемого вещества, чтобы она находилась в электрическом поле максимальной напряженности?

D2  ^0.30 Вычислите фактор усиления $g(\omega)$ электрического поля в этой точке, $g(\omega)=\underset{\vec{r}}{\max}\frac{\left|\vec{E}(\vec{r})\right|}{\left|\vec{E}_0\right|}$. Ответ выразите через диэлектрическую проницаемость металла $\varepsilon(\omega)$.

Металлическая частица усиливает не только исходное излучение с амплитудой $\left|\vec{E}_0\right|$, но также и дипольное излучение, которое генерирует молекула. Этот процесс также можно охарактеризовать фактором усиления $g'(\omega, \omega_0)$. Если частота $\omega$ внешнего поля велика по сравнению с частотой $\omega_0$ собственных колебаний молекулы, можно считать $g'\approx{g}$. Тогда интенсивность сигнала в эксперименте SERS возрастает по сравнению с обычной рамановской спектроскопией в $g^4$ раз.

В реальных экспериментах для усиления сигнала обычно исследуют не одну молекулу, а сразу большое их количество. Излучения различных молекул в таких экспериментах не когерентны, поэтому суммарная интенсивность излучения от $N$ молекул равна $NI_0$, где $I_0$ — интенсивность излучения от одной молекулы. Пример результатов таких измерений изображен на рис. 3.

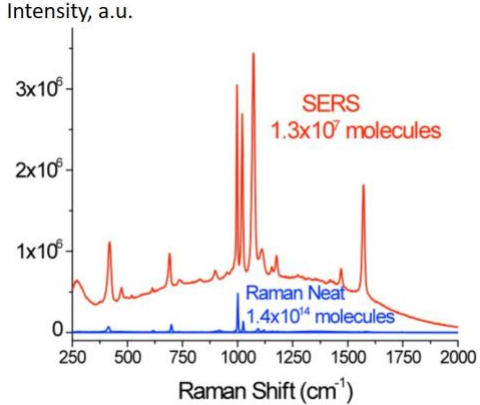
Спектр рамановского сигнала. Верхняя кривая отвечает эксперименту SERS,нижняя — обычной рамановской спектроскопии. По горизонтальной оси отложена величина рамановского сдвига, $k_0=\omega_0/c$, по вертикальной – интенсивность излучения в произвольных единицах. Обратим внимание, что в этих двух экспериментах в формировании сигнала участвовало разное число
молекул, см. подписи на графике.

D3  ^1.40 Из экспериментальных данных, приведенных на рисунке выше, оцените фактор усиления $g$ электрического поля вследствие плазмонного резонанса (рассмотрите пик при рамановском сдвиге $\omega_0/c=1000 \text{см}^{-1}$). Считайте, что условие $\omega_0\ll{\omega}$ выполнено.

D4  ^0.50 Пользуясь результатами второй части задачи, оцените размер $R$ металлических частиц, использовавшихся в эксперименте, если длина волны падающего излучения $\lambda=785 \text{нм}$.