A1  ^1.10 Электрическое поле приводит к согласованному смещению $\vec{r}(t)$ электронов в направлении поля. Определите зависимость $\vec r(t)$ и вектор поляризации среды $\vec P(t)$ в установившемся режиме.

Запишем второй закон Ньютона для электрона, движущегося в указанном поле ($e > 0$):
$$m \frac{d^2}{d t^2} \vec{r}(t)=-e \vec{E}_0 \sin (\omega t)$$
Интегрируя уравнение движения, с условиями, что координата и скорость ограничены при $t\to\infty$, получаем ответ на первый вопрос

A2  ^0.30 Вычислите диэлектрическую проницаемость металла $\varepsilon(\omega)$ и постройте график этой зависимости.

Используя соотношения между вектором электрической индукции, напряженности и поляризации, получим:
$$\varepsilon_0\varepsilon(\omega)\vec E_0=\varepsilon \vec E_0 + \vec P,$$
учитывая ответ пункта A1, получаем ответ:

B1  ^2.60 Определите поле $\vec{E}_{in}$ внутри шара и его дипольный момент $\vec{d}_0$ .

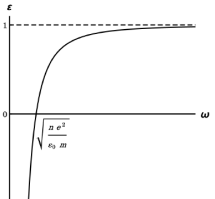
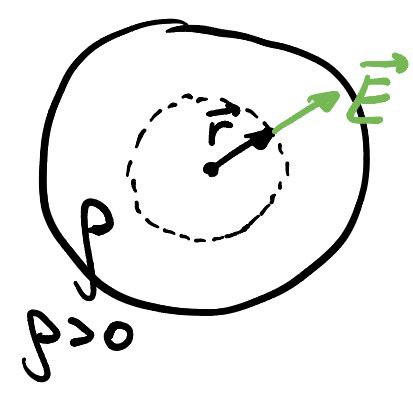
Этот пункт задачи представляет собой классическую задачу по нахождению поля внутри диэлектрического шара, помещенного в постоянное электрическое поле. Одно из решений приводится ниже.

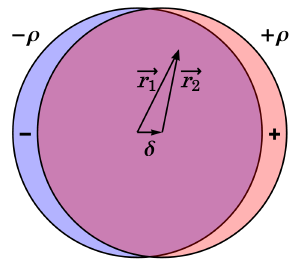
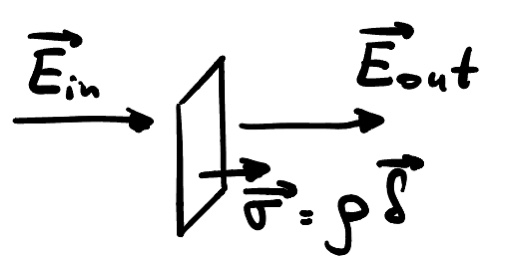
Дипольный момент системы равен заряду шаров, умноженному на вектор $\vec\delta$, т.е.
$$\vec d_0=\cfrac{4}{3}\pi R^3\rho\cdot \vec\delta=\cfrac{4}{3}\pi R^3\vec\sigma,$$
а вектор $\vec\sigma$ также получим из решения системы уравнений выше. Таким образом:

B2  ^0.70 Нарисуйте картину силовых линий электрического поля в системе (внутри, вблизи и вдали от шара), считая $\varepsilon(\omega)=-3$.

B3  ^0.20 При некотором значении $\varepsilon(\omega_{res})=\varepsilon_{res}$ амплитуда электрического поля внутри шара $\left|\vec{E}_{in}\right|$ начинает неограниченно возрастать. Определите значение $\varepsilon_{res}$.

B4  ^0.60 Осциллирующий диполь излучает энергию. Оцените мощность $I$ этих потерь, используя анализ размерностей и тот факт, что интенсивность дипольного излучения зависит только от амплитуды дипольного момента $\left|\vec{d}_0\right|$, частоты его колебаний $\omega_{res}$, скорости распространения волн c и электрической постоянной $\varepsilon_0$.

$$I=\varepsilon_0^\alpha\cdot |\vec d_{sp}|^\beta\cdot \omega_{res}^\gamma\cdot c^\zeta$$
Запишем размерности величин
$[I] = Н\cdot м\cdot с^{-1}$
$[\varepsilon_0]=Кл^2\cdot Н^{-1}\cdot м^{-2}$
$[d]=Кл\cdot м$
$[\omega]=с^{-1}$
$[c] = м\cdot с^{-1}$
Решая систему, получим $\alpha=-1, \beta=2, \gamma=4, \zeta=-3$.

B5  ^3.80 Оцените среднюю энергию, вкачиваемую в систему за счет внешнего поля в условиях плазмонного резонанса при $\omega=\omega_{res}$. Из условия баланса энергии оцените амплитуду поля внутри шара в резонансе.

Оценим энергию, вкачиваемую в систему, как среднюю потенциальную энергию диполя за период.
$$W=-(\vec d, \vec E)=d_0E_0\cos^2\omega t=\cfrac{d_0E_0}{2}(1-\cos 2\omega t)$$
$$\overline W=\cfrac{d_0E_0}{2}$$
Таким образом, средняя мощность за период равна
$$P=\overline W/T=\cfrac{d_0E_0\omega_{res}}{4\pi}$$
и с точностью до множителя может быть оценена как
$$P\sim d_0 E_0 \omega_{res}.$$

В равновесном случае вкачиваемая мощность должна уноситься излучением $P=I$ или
$$ d_0 E_0 \omega_{res}=\frac{\left|\vec{d}_{0}\right|^2 \omega_{\text {res }}^4}{\varepsilon_0 c^3},$$
учитывая, что $d_0=\varepsilon_0 E_{in}R^3$ из пункта B1, получаем ответ:

C1  ^0.70 Рассмотрим два грузика с массами $m_1$ и $m_2$, соединенные между собой пружиной с жесткостью $k$. Определите частоту $\omega_0$ малых колебаний в системе.

C2  ^0.20 Считая малой амплитуду механических колебаний около положения равновесия, напишите явное выражение для $\alpha(x)$ в линейном приближении, если $\alpha(0)=\alpha_0$ и $\frac{d\alpha}{dx}\bigg|_{x=0}=\beta_0$.

C3  ^0.20 Вычислите дипольный момент двухатомной молекулы во внешнем поле $\vec{E}_0\cos\omega t$. Ответ представьте в виде:
$$\vec{d}=\sum_i\vec{d}_i\cos\omega_it
$$

$$d = \varepsilon_0(\alpha_0 + \beta_0 x_0 \cos\omega_0 t)E_0\cos \omega t,$$
что, раскрывая скобки, даст ответ

C4  ^0.20 Детектор регистрирует дипольное излучение молекулы. Выражению из предыдущего пункта будут соответствовать несколько пиков на частотах $\omega_i$. Высота каждого пика равна интенсивности излучения отдельного диполя $\vec{d}_i$ . Для каждого пика определите его частоту и высоту. Выразите ответ через $\varepsilon_0$, $\alpha_0$, $\beta_0$, $x_0$, $\omega$, $\omega_0$ и $\vec{E}_0$.

Используя найденное в пункте B4 значение интенсивности излучения, для каждой из частот из пункта C3 получим

D1  ^1.20 В какую точку пространства нужно поместить молекулу исследуемого вещества, чтобы она находилась в электрическом поле максимальной напряженности?

Максимальное поле будет в двух точках, где сонаправлены внешнее поле $\vec E_0$ и поле диполя, создаваемое шаром. Это диаметрально противоположные точки шара, причем диаметр выбран коллинеарным полю $\vec E_0$.

D2  ^0.30 Вычислите фактор усиления $g(\omega)$ электрического поля в этой точке, $g(\omega)=\underset{\vec{r}}{\max}\frac{\left|\vec{E}(\vec{r})\right|}{\left|\vec{E}_0\right|}$. Ответ выразите через диэлектрическую проницаемость металла $\varepsilon(\omega)$.

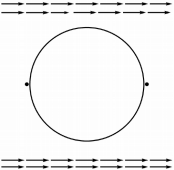
В обозначениях пункта B1 в задании спрашивается отношение $E_{out}/E_0$, т.е.
$\cfrac{E_{out}}{E_0}=\cfrac{\varepsilon(\omega)E_{in}}{E_0}=\cfrac{3\varepsilon(\omega)}{\varepsilon(\omega) + 2}$

D3  ^1.40 Из экспериментальных данных, приведенных на рисунке выше, оцените фактор усиления $g$ электрического поля вследствие плазмонного резонанса (рассмотрите пик при рамановском сдвиге $\omega_0/c=1000~\text{см}^{-1}$). Считайте, что условие $\omega_0\ll{\omega}$ выполнено.

Снимем величины, которые понадобятся для расчетов, из графика:
$$I_{SERS}=3\cdot 10^6~у.е.$$ $$I_{Raman}=0.45\cdot 10^6~у.е.$$ $$N_{SERS} = 1.4\cdot 10^7$$ $$N_{Raman}=1.3\cdot 10^{14}$$
Рассчитаем фактор усиления
$$g=\sqrt[4]{\cfrac{I_{SERS}/N_{SERS}}{I_{Raman}/N_{Raman}}}$$

D4  ^0.50 Пользуясь результатами второй части задачи, оцените размер $R$ металлических частиц, использовавшихся в эксперименте, если длина волны падающего излучения $\lambda=785~\text{нм}$.

Используя ответы пунктов B5 и D2, получаем:
$$\cfrac{E_{in}}{E_0}=\cfrac{g(\omega_{res})}{|\varepsilon(\omega_{res})|}=\left(\cfrac{c}{\omega_{res} R}\right)^3=\left(\cfrac{\lambda}{2\pi R}\right)^3,$$ откуда
$$R\sim \cfrac{\lambda}{2\pi (g/\varepsilon)^{1/3}}.$$
Расчеты произведем для $g=92, |\varepsilon|=2, \lambda=735~нм$ и получим