A1  ^0.70 Получите точное выражение для угловой скорости орбитального вращения $\omega$.
Ответ выразите через $G, m, M$ и $L$.

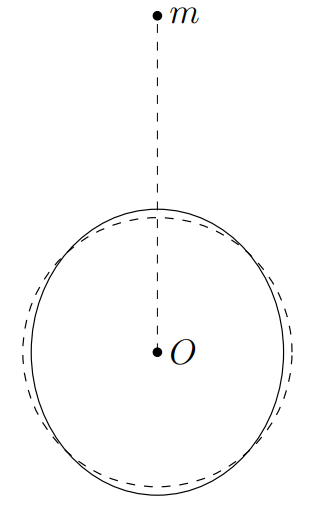
Пусть $\vec{e}_1$ - единичный вектор, проведённый направленный на меньшее тело из центра большего. Ускорения тел за счет гравитации:
$$\vec{a}_m=-\cfrac{GM}{L^2}\vec{e}_1\quad \vec{a}_M=\cfrac{Gm}{L^2}\vec{e}_1; \quad {\vec{a}_M-\vec{a}_m=\cfrac{G(M+m)}{L^3}\vec{e}_1}.
$$
С другой стороны:
$$\vec{a}_M-\vec{a}_m=\omega^2L\vec{e}_1,
$$
откуда окончательно:

A2  ^0.20 Получите точное выражение для разности потенциалов гравитационного поля малого тела $\Delta{\varphi}_\text{гр}=\varphi_{\text{гр}P}-\varphi_{\text{гр}O}$ в точках $P$ и $O$. Ответ выразите через $G$, $m$, $L$, $\theta$ и $r(\theta)$.

Потенциал поля малого тела в точке, расстояние до которой от неё равно $L_m$, равен:
$$\varphi_\text{гр}=-\cfrac{Gm}{L_m}
$$
Найдём расстояние от малого тела до точки $A$ по теореме косинусов:
$$L^2_m=L^2+r^2(\theta)-2Lr(\theta)\cos\theta
$$
Окончательно имеем:

A3  ^0.50 Получите точное выражение для разности потенциалов сил инерции $\Delta{\varphi}_\text{ин}=\varphi_{\text{ин}P}-\varphi_{\text{ин}O}$ в точках $P$ и $O$. Ответ выразите через $G$, $m$, $M$, $L$, $\theta$ и $r(\theta)$.

Поскольку жидкость неподвижна, а большее тело вращается с постоянной угловой скоростью - вклад в разность потенциалов вносят поля сил инерции $-\Delta{m}\vec{a}_0$ и $\Delta{m}\omega^2\vec{r}_\perp$, действующие на частицу массой $\Delta{m}$.
Для разности потенциалов точек $A$ и $O$ имеем:
$$\varphi_{\text{ин}A}-\varphi_{\text{ин}O}=-\int\limits_{O}^{A}(\omega^2\vec{r}_\perp-\vec{a}_0)\cdot d\vec{r}
$$
Учитывая, что $\vec{a}_0=Gm\vec{e}_1/L^2$, а $\vec{r}_\perp=\vec{r}$:
$$\varphi_{\text{ин}A}-\varphi_{\text{ин}O}=-\int\limits_{O}^{A}(\omega^2\vec{r}-\cfrac{Gm}{L^2}\vec{e}_1)\cdot d\vec{r}=\cfrac{Gmr\cos\theta}{L^2}-\cfrac{\omega^2r^2}{2}
$$
Окончательно:

A4  ^1.30 Получите зависимость $h(\theta)$. Ответ выразите через $m$, $M$, $R$, $L$ и $\theta$. Максимально упростите ваш ответ. Качественно изобразите форму поверхности в рассматриваемом сечении. На этом же рисунке изобразите невозмущённую форму поверхности. 

 

Примечание: воспользуйтесь следующим приближением: $$\cfrac{1}{\sqrt{1+a^2-2a\cos\theta}}\approx{1+a\cos\theta+\cfrac{a^2(3\cos^2\theta-1)}{2}} $$

Поверхность большего тела в равновесии эквипотенциальна. Так как возмущения поверхности малы, будем считать, что потенциал гравитационного поля большего тела на поверхности равен:
$$\varphi_M=-\cfrac{GM}{r(\theta)}
$$
Поскольку поверхность эквипотенциальна:
$$\varphi_A=Gm\left(\cfrac{1}{L}-\cfrac{1}{\sqrt{L^2+r^2-2rL\cos\theta}}\right)+\cfrac{Gmr\cos\theta}{L^2}-\cfrac{G(M+m)r^2}{2L^3}-\cfrac{GM}{r(\theta)}+C_1=C_2
$$
где $C_1$ и $C_2$ - некоторые постоянные величины.
Раскладывая выражение под корнем:
$$\cfrac{1}{\sqrt{L^2+r^2-2rL\cos\theta}}\approx{\cfrac{1}{L}\left(1+a\cos\theta+\cfrac{a^2(3\cos^2\theta-1)}{2}\right)};\quad a=\cfrac{r}{L}.
$$
Таким образом, имеем:
$$-\cfrac{GM}{r}-\cfrac{G(M+3m\cos^2\theta)r^2}{2L^3}=const
$$
Заметим, что слагаемые, пропорциональные $\cos \theta$ полностью сократились. Из-за этого и потребовалось раскладывать потенциал малого тела до второго порядка.
Далее подставим $r=R+h$ и разложим до первого порядка потенциал большого тела. В потенциале малого тела можно сразу считать $r = R$, так как он сам является малой величиной из-за условия $R \ll L$. Получим
$$-\cfrac{GM}{R}+\cfrac{GMh}{R^2}-\cfrac{G(M+3m\cos^2\theta)R^2}{2L^3}=const.
$$
Оставим только переменные слагаемые:
$$h\cfrac{GM}{R^2}-\cfrac{3GmR^2\cos^2\theta}{2L^3}=const
$$
Поскольку $h(\pi/2)=0$, последняя константа равна нулю. Тогда имеем:

B1  ^0.50 Покажите, что касательную компоненту силы $F_\tau(t,\, \theta)$, действующую на частицу массой $\Delta{m}$, находящуюся на поверхности большего тела под углом $\theta$, можно представить в виде: $$F_\tau(t,\,\theta)=\Delta{m}\alpha\sin(2\omega_1t-2\theta) $$ Найдите $\alpha$. Ответ выразите через $G$, $m$, $L$ и $r(\theta)$.

 

Примечание: воспользуйтесь результатами, полученными при решении пункта $\mathrm{A4}$.

В пункте $\mathrm{A4}$ нами было получено приближённое выражение для потенциала сил инерции и гравитационного поля меньшего тела:
$$\varphi_\text{внеш}=-\cfrac{G(M+3m\cos^2\theta)r^2}{2L^3}
$$
Тогда для компоненты силы $F_\tau$ получим:
$$F_\tau=-\cfrac{\Delta{m}}{r}\cfrac{\partial{\varphi_\text{внеш}}}{\partial{\theta}}=-\cfrac{3Gm\Delta{m}r\sin2\theta}{2L^3}
$$
Отметим, что эта компонента силы возникает из-за неоднородности гравитационного поля меньшего тела.
Поскольку $\omega\neq{\Omega}$, в произвольный момент времени $t$ параметр $\theta$ равен:
$$\theta=\theta_0-\omega_1 t, \quad \omega_1 = \omega - \Omega.
$$
Также учтем, что с нужной нам точностью $r \approx R$. Тогда окончательно имеем:
$$F_\tau(t{,}\theta_0)=\cfrac{3Gm\Delta{m}R}{2L^3}\sin\left(2\omega_1 t-2\theta_0\right)
$$

B2  ^0.80 Покажите, что зависимость $\theta(t{,}\theta_0)$ имеет следующий вид:
$$\theta(t)=\theta_0+A\sin(2\omega_1t-2\theta_0-\varphi_0)
$$
Найдите $A$ и $\varphi_0$. Ответы выразите через $G$, $m$, $L$, $\gamma$, $\omega_0$, $\omega$, $\Omega$ и $\theta_0$.

Подставим $F_\tau(t{,}\theta)$ в уравнение движения:
$$\Delta{m}r^2\left(\ddot{\theta}+2\gamma\dot{\theta}+\omega^2_0(\theta-\theta_0)\right)=rF_\tau(t{,}\theta)=\Delta{m}r^2\cdot\cfrac{3Gm}{2L^3}\sin\left(2\omega_1 t-2\theta\right)
$$
Поскольку $\omega^2_0\gg{Gm/L^3}$ - можно считать, что $F_\tau(t{,}\theta)\approx{F_\tau(t{,}\theta_0)}$. Тогда:
$$\ddot{\theta}+2\gamma\dot{\theta}+\omega^2_0(\theta-\theta_0)=\cfrac{3Gm}{2L^3}\sin\left(2\omega_1 t-2\theta_0\right)
$$
Решение уравнения будем искать в виде $\theta(t) =\theta_0 + Re\left(\hat{A}e^{2i(\omega-\Omega)t}\right)$:
$$\left(\omega^2_0-4\omega_1^2+4i\omega_1\gamma\right)\hat{A}=\cfrac{3Gm}{2L^3}e^{-i(2\theta_0+\pi/2)}
$$
Представим $\hat{A}$ в показательной форме $\hat{A}=Ae^{-i\varphi_0}$, где:

B3  ^0.40 Получите выражение для скорости роста высоты $\dot{h'}(t{,}\,\theta_0)$ в момент времени $t$ при угле $\theta_0$. Ответ выразите через $h_0$ и $\frac{d\dot{\theta}}{d\theta _0}$

Объем жидкости, втекающей через одну из граней $hdz$ за время $dt$ равен произведению скорости течения $\dot{\theta} R$ на площадь $hdz$ и рассматриваемое время $dt$:
$$
dV_1 = \dot{\theta} R h dz dt \approx \dot{\theta} R h_0 dz dt.
$$
Здесь мы учитываем, что высота поверхности воды меняется мало, и это практически не влияет на поток воды.
Скорости течения, отвечающие углам $\theta_0$ и $\theta_0 + d \theta_0$ несколько отличаются, поэтому разность втекающего и вытекающего объемов воды
$$
dV = \dot{\theta}(\theta_0) R h_0 dz dt -\dot{\theta}(\theta_0+ d\theta_0) R h_0 dz dt = -Rh_0 \frac{\partial \dot{\theta}}{\partial \theta_0}d\theta_0 dz dt.
$$
Из-за этого меняется высота поверхности жидкости:
$$
dV = Rd\theta_0 dz dh = R d\theta_0 dz \dot{h} dt = -Rh_0 \frac{\partial \dot{\theta}}{\partial \theta_0}d\theta_0 dz.
$$
Отсюда $\dot{h} = - h_0\dfrac{\partial \dot{\theta}}{\partial \theta_0}$, а поскольку $h_0 = const$

B4  ^0.30 Считая, что амплитуда колебаний $h'$ одинакова для всех значений $\theta_0$, получите зависимость $h(t)$. Ответ выразите через $h_0$, $A$, $\omega_1$, $\varphi_1$ и $t$.

Из результатов пункта $\mathrm{B2}$ получим:
$$\theta=\theta_0 + A\sin(2\omega_1t-\varphi_1), \quad {\dot\theta=2\omega_1A\cos(2\omega_1t-\varphi_1)}.$$
Тогда находим
$${\cfrac{\partial\dot\theta(t,\theta_0)}{\partial\theta_0}=4\omega_1A\sin(2\omega_1t-\varphi_1)},
$$
откуда:
$$\dot{h'}=-4h_0\omega_1A\sin(2\omega_1t-\varphi_1)
$$
Интегрируя, находим:

B5  ^0.40 Для момента времени $t$ определите значения углов $\theta_0$, соответствующих максимальному значению $h(t{,}\,\theta_0)$. Ответы выразите через $\omega_1$, $t$ и $\varphi_0$.

В точках максимума косинус равен единице, поэтому:
$$2\omega_1t-\varphi_1=0{;}\,2\pi.
$$
Подставляя $\varphi_1$, находим:

B6  ^1.40 Найдите момент сил $M_z$, действующий со стороны малого тела на поверхность большого относительно оси $z$. Ответ выразите через $G$, $m$, $\rho$, $R$, $h_0$, $L$, $A$ и $\varphi_0$.

Плечо силы, соответствующее углу $\beta$, равно $R\sin\beta$. Тогда для элемента момента силы $dM_z$ имеем:
$$dM_z=R\sin\beta dF_\tau(t{,}\theta{,}\beta)
$$
Для $dF_\tau$ также имеем:
$$dF_\tau=\cfrac{3GmR\sin\beta}{2L^3} \Delta m \sin(2\omega_1t-2\theta).
$$
Масса рассматриваемого объема
$$
\Delta m = \rho dV = \rho h(t,\, \theta,\, \beta) dS = \rho h(t,\, \theta,\, \beta) R^2 \sin \beta d\beta d\theta.
$$
Тогда получим:
$$dF_\tau=\cfrac{3GmR\sin\beta}{2L^3} \sin(2\omega_1t-2\theta) \rho h(t,\, \theta,\, \beta) R^2 \sin \beta d\beta d\theta.
$$
Для $h(t{,}\theta{,}\beta)$ имеем:
$$h(t,\,\theta,\,\beta)=h_0(1+2A\cos(2\omega_1t-\varphi_1))
$$
так как $A$ не зависит от расстояния до оси $z$.
Представим выражение для $M_z$ в виде интеграла:
$$M_z=\cfrac{3Gm\rho R^4h_0}{2L^3}\int\limits_0^{\pi}\sin^3\beta d\beta\int\limits_0^{2\pi}(1+2A\cos(2\omega_1t-\varphi_1))\sin(2\omega_1t-2\theta)d\theta
$$
Для интеграла по $\beta$ имеем:
$$\int\limits_0^{\pi}\sin^3\beta d\beta=\int\limits_{-1}^{1}(1-\cos^2\beta)d\cos\beta=\cos\beta-\cfrac{\cos^3\beta}{3}\bigg|_{-1}^{1}=\cfrac{4}{3}
$$
Поэтому:
$$M_z=\cfrac{2Gm\rho R^4h_0}{L^3}\int\limits_0^{2\pi}(1+2A\cos(2\omega_1t-\varphi_1))\sin(2\omega_1t-2\theta)d\theta
$$
Второй интеграл берётся за период, поэтому для функции $\sin(2\omega_1t-2\theta)$ он равен нулю.
Перейдём к последнему интегралу:
$$\int\limits_0^{2\pi}\cos(2\omega_1t-\varphi_1)\sin(2\omega_1t-2\theta)d\theta=\int\limits_0^{2\pi}\cos(2\omega_1t-2\theta-\varphi_0)\sin(2\omega_1t-2\theta)d\theta
$$
Воспользуемся тригонометрической формулой:
$$\sin\alpha\cos\beta=\cfrac{\sin(\alpha+\beta)+\sin(\alpha-\beta)}{2}
$$
Получим:
$$M_z=\cfrac{2Gm\rho R^4h_0A}{L^3}\int\limits_0^{2\pi}[\sin(4\omega_1t-4\theta-\varphi_0)+\sin\varphi_0]d\theta
$$
Окончательно:

C1  ^0.80 Найдите орбитальную угловую скорость вращения $\omega_\text{синх}$ и расстояние $L_\text{синх}$ между Землёй и Луной при синхронном вращении. Выразите ответы через $m$,$M$, $R$, $G$, $L_0$, $\Omega_0$ и найдите их численные значения.

 

Примечание: при синхронном вращении моментом импульса Земли, связанным с вращением вокруг ее оси, можно пренебречь.

Воспользуемся законом сохранения момента импульса, который обозначим за $K$:
$$K=I\Omega_0+\cfrac{mML^2_0\omega_0}{M+m}=const
$$
где $I=2MR^2/5$ - момент инерции Земного шара относительно диаметра.
В установившемся режиме $\Omega=\omega=\omega_\text{синх}$, поэтому:
$$K=\omega_\text{синх}\left(I+\cfrac{mML^2_\text{синх}}{m+M}\right)
$$
Поскольку при синхронном вращении Землю можно считать материальной точкой:
$$K\approx{\cfrac{mML^2_\text{синх}\omega_\text{синх}}{m+M}}
$$
Используя соотношение
$$\omega^2=\cfrac{G(M+m)}{L^3}
$$
получим:
$$K\approx\cfrac{G^{2/3}Mm}{(m+M)^{1/3}\omega^{1/3}_\text{синх}}
$$
откуда окончательно:

C2  ^0.70 Расстояние между Землей и Луной увеличивается со скоростью $\dot{L}_{0}=1~\text{см}/\text{год}$.
Найдите величину среднего углового ускорение Земли $\dot{\Omega}_0$.
Выразите ответ через $m$,$M$, $R$, $G$, $L_0$, $\Omega_0$, $\dot{L}_0$ и найдите его численное значение.

Момент импульса системы $K$ с помощью связь $\omega$ и $L$ приводится к виду:
$$K=I\Omega+\cfrac{mML^2}{m+M}\sqrt{\cfrac{G(m+M)}{L^3}}
$$
Дифференцируя, находим:
$$I\dot{\Omega}+\cfrac{mM}{2(m+M))}\sqrt{\cfrac{G(m+M)}{L}}\dot{L}=0
$$
откуда:

C3  ^0.80 Найдите численные значения $\omega_0$ и $\gamma$.

В пункте $\mathrm{B5}$ было получено, что положение прилива отстаёт от Луны на угол $\varphi_0/2$ по направлению вращения Луны относительно Земли. Тогда имеем:
$$2\beta=\arctan\cfrac{-4\omega_1\gamma}{\omega^2_0-4\omega^2_1}=-\varphi_0
$$
Также для разницы высот прилива и отлива имеем:
$$\Delta{h}=h_\text{пр}-h_\text{от}=4Ah_0
$$
или, после подстановки выражения для $A$:
$$\Delta{h}=\cfrac{6Gmh_0}{L^3_0\sqrt{(\omega^2_0-4\omega^2_1)^2+16\omega^2_1\gamma^2}}=\cfrac{6Gmh_0\cos 2\beta}{L^3_0(\omega^2_0-4\omega^2_1)}
$$
Находим:

C4  ^0.50 В рамках описанной модели найдите угловое ускорение Земли $\dot{\Omega}_{0\text{(мод)}}$, которое получается из результатов пункта $\mathrm{B6}$.
Сравните его со значением $\dot{\Omega}_0$, полученным в пункте $\mathrm{C2}$ и сделайте вывод о применимости рассматриваемой модели (считайте модель применимой, если $\Omega_0$ и $\Omega_{0\text{(мод)}}$ отличаются не более, чем в 10 раз).

Из уравнения динамики вращательного движения относительно центра масс получим:
$$I\dot{\Omega}=M_z=\cfrac{4\pi Gm\rho R^4h_0A\sin\varphi_0}{L^3}
$$
Далее обратим внимание, что $h_0A=\Delta{h}/4$, а $\varphi_0=-2\theta$. Тогда имеем:

C5  ^0.70 Оцените численное значение $\tau_2$. Ответ выразите в годах.

После перехода к режиму синхронного вращения можно считать, что:
$$\omega=const\quad L=const\quad \omega^2_0\gg\omega^2_1
$$
Поэтому:
$$I\dot{\Omega}=M_z=\cfrac{4\pi Gm\rho R^4h_0A\sin\varphi_0}{L^3}\approx\cfrac{4\pi Gm\rho{R}^4h_0}{L^3_\text{синх}}\cdot{\cfrac{3Gm}{2L^3_\text{синх}\omega^2_0}}\cdot\cfrac{4(\omega_\text{синх}-\Omega)\gamma}{\omega^2_0}
$$
откуда:
$$d\tau_2=-\cfrac{d\Omega}{\Omega-\omega_\text{синх}}\cdot{\cfrac{ML^6_\text{синх}\omega^4_0}{120\pi G^2m^2\rho{R}^2h_0\gamma}}
$$
откуда: