Часть A. Центральные соударения без диссипаций (2.0 балла)

В этой части задачи все столкновения являются центральными. Диссипаций в системе нет.

A1  ^0.30 Определите момент инерции системы из стержня и сфер относительно оси вращения. Ответ выразите через $m$ и $l$.

A2  ^0.50 Выразите угловую скорость $\omega_{i+1}$ системы после столкновения с $i+1$-ым вылетевшим шариком через $\omega_i$, $v$ и $l$.

A3  ^0.20 Чему равна $\omega_1$? Ответ выразите через $v$ и $l$.

Как можно ожидать, угловая скорость такой вращающейся системы стремится при $i\to{\infty}$ к постоянному значению $\omega^*$.

A4  ^0.20 Выразите $\omega^*$ через $v$ и $l$.

A5  ^0.60 Решив рекуррентное уравнение, полученное в пункте $\bf A1$, получите явное выражение для $\omega_i$. Ответ выразите через $i$, $v$ и $l$.

Подсказка: воспользуйтесь переменной $\omega'_i=\omega_i-v/l$. 

Пусть теперь вместо одной пары сфер их у нас будет две пары, размещённые на стержнях, перпендикулярных друг другу и оси.

A6  ^0.20 Каким будет предельное значение $\omega^*$ для такой системы?

Часть B. Нецентральные соударения без диссипаций (3.0 балла)

B1  ^1.00 При каком значении параметра $k_0$ скорость первого вылетевшего шарика сразу после столкновения со сферой будет направлена горизонтально?

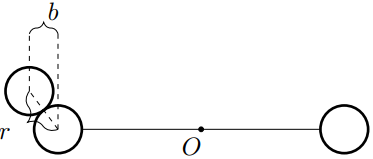
Далее рассматривается произвольное значение параметра $k$.

B2  ^1.00 Выразите угловую скорость $\omega_{i+1}$ системы после столкновения с $i+1$-ым вылетевшим шариком через $\omega_i$, $v$, $l$ и $k$.

B3  ^0.20 Чему равна $\omega_1$? Ответ выразите через $v_0$, $l$ и $k$.

B4  ^0.80 Решив рекуррентное уравнение, полученное в пункте $\bf B2$, получите явное выражение для $\omega_i$. Ответ выразите через $i$, $v$ и $l$.

Часть C. По мотивам Коткина—Сербо (4.0 балла)

В данной части задачи изучается движение системы под воздействием трения. Под действием трения этом на систему действует момент $M$, являющийся некоторой функцией угловой скорости $\omega$. В зависимости от геометрии системы, основной вклад даёт:

1. Сухое трение — момент $M=\alpha I=\operatorname{const}$;
2. Линейное вязкое трение — момент $M=\beta I\omega$, $\beta=\operatorname{const}$;
3. Квадратичное вязкое трение — момент $M=\gamma I\omega^2$, $\gamma=\operatorname{const}$.

Здесь $I$ — момент инерции системы. Вместо момента инерции системы и скорости шарика введём параметры $\varepsilon=\frac{ml^2}I$ и $\omega_0=\cfrac vl$. Во всех пунктах части C соударения являются центральными и упругими.

Все ответы в пунктах C1–C3 выразите через $\varepsilon$ и $\omega_0$.

C1  ^0.50 Найдите, при каких значениях параметра $\alpha$ система в режиме сухого трения будет продолжать движение неограниченно долго после первого столкновения с шариком.

C2  ^0.50 Найдите, при каких значениях параметра $\beta$ система в режиме линейного вязкого трения будет продолжать движение неограниченно долго после первого столкновения с шариком.

C3  ^0.50 Найдите, при каких значениях параметра $\gamma$ система в режиме квадратичного вязкого трения будет продолжать движение неограниченно долго после первого столкновения с шариком.

Приступим теперь непосредственно к точному вычислению установившихся средних угловых скоростей в каждом из трёх режимов. Для этого совместно с уравнением для столкновения с шариком нужно решить уравнение свободного движения системы и найти стационарные точки.

C4  ^0.70 Найдите установившуюся среднюю по периоду угловую скорость системы $\overline\omega_1$ в режиме сухого трения. Выразите ответ через $\varepsilon$, $\alpha$ и $\omega_0$.

Ответы в пунктах C5 и C6 выразите через $\varepsilon$, $\beta$ и $\omega_0$.

C5  ^0.50 Найдите стационарное значение угловой скорости $\omega^\uparrow_2$ системы непосредственно после очередного столкновения с шариком в режиме линейного вязкого трения.

C6  ^0.40 Найдите установившуюся среднюю по периоду угловую скорость системы $\overline\omega_2$ в режиме линейного вязкого трения.

Ответы в пунктах C7 и C8 выразите через $\varepsilon$, $\gamma$ и $\omega_0$.

C7  ^0.50 Найдите стационарное значение угловой скорости $\omega^\uparrow_3$ системы непосредственно после очередного столкновения с шариком в режиме квадратичного вязкого трения.

C8  ^0.40 Найдите установившуюся среднюю по периоду угловую скорость системы $\overline\omega_3$ в режиме квадратичного вязкого трения.