A1  ^0.30 Определите момент инерции системы из стержня и сфер относительно оси вращения. Ответ выразите через $m$ и $l$.

Момент инерции каждой сферы относительно оси вращения равен $ml^2$, поскольку их размерами можно пренебречь.
Исходный стержень эквивалентен двум другим с массой $2m$ и длиной $l$.
Момент инерции стержня массой $M$ и длиной $L$ относительно оси, проходящей перпендикулярно стержню через его конец, равен:
$$I_\text{ст}=\cfrac{ML^2}{3}
$$
Тогда момент инерции $I$ системы относительно оси вращения равен:

A2  ^0.50 Выразите угловую скорость $\omega_{i+1}$ системы после столкновения с $i+1$-ым вылетевшим шариком через $\omega_i$, $v$ и $l$.

Воспользуемся законами сохранения энергии и момента импульса относительно оси вращения:
$$\begin{cases}
E=\cfrac{mv^2}{2}+\cfrac{I\omega^2_i}{2}=\cfrac{mu^2}{2}+\cfrac{I\omega^2_{i+1}}{2}\\
L=mvl+I\omega_i=mul+I\omega_{i+1}
\end{cases}
$$
Здесь $u$ - скорость налетающего шарика сразу после удара, по направлению совпадающая со скоростью $v$.
Исключим из системы $u$:
$$u=v-\cfrac{I(\omega_{i+1}-\omega_i)}{ml}\Rightarrow I(\omega^2_{i+1}-\omega^2_i)=v^2-\left(v-\cfrac{I(\omega_{i+1}-\omega_i)}{ml}\right)^2
$$
Сокращая корень $\omega_{i+1}=\omega_i$, получим:
$$\omega_{i+1}\left(1+\cfrac{I}{ml^2}\right)+\omega_{i}\left(1-\cfrac{I}{ml^2}\right)=\cfrac{2v}{l}
$$
Таким образом:

A3  ^0.20 Чему равна $\omega_1$? Ответ выразите через $v$ и $l$.

Поскольку $\omega_0=0$, находим:

A4  ^0.20 Выразите $\omega^*$ через $v$ и $l$.

Приравнивая $\omega_{i+1}$ и $\omega_i$, находим:

A5  ^0.60 Решив рекуррентное уравнение, полученное в пункте $\bf A1$, получите явное выражение для $\omega_i$. Ответ выразите через $i$, $v$ и $l$.

Подсказка: воспользуйтесь переменной $\omega'_i=\omega_i-v/l$. 

Уравнение, полученное в пункте $\mathrm{A1}$, приводится к следующему виду:
$$13\left(\omega_{i+1}-\cfrac{v}{l}\right)=7\left(\omega_i-\cfrac{v}{l}\right)
$$
Вводя переменную $\omega'_i=\omega_i-v/l$, получим:
$$13\omega'_{i+1}=7\omega'_i
$$
Откуда:
$$\omega'_i=\omega'_1\cdot{\left(\cfrac{7}{13}\right)^{i-1}}
$$
Поскольку $\omega_0=0$, $\omega_1=6v/(13l)$. Тогда $\omega'_1=-7v/(13l)$, откуда :
$$\omega'_i=-\cfrac{v}{l}\left(\cfrac{7}{13}\right)^i
$$
и окончательно

A6  ^0.20 Каким будет предельное значение $\omega^*$ для такой системы?

Обратим внимание, что если в рекуррентном уравнении, полученном в пункте $\mathrm{A1}$, положить $\omega_{i+1}=\omega_i$, то при любых значениях момента инерции $I$ получится значение:

B1  ^1.00 При каком значении параметра $k_0$ скорость первого вылетевшего шарика сразу после столкновения со сферой будет направлена горизонтально?

Пусть $u$ - скорость вылетающего шарика сразу после удара. Поскольку она направлена горизонтально - сразу после удара момент импульса вылетающего шарика относительно оси вращения равен нулю.
Тогда законы сохранения энергии и момента импульса записываются следующим образом:
$$\begin{cases}
E=\cfrac{mv^2}{2}=\cfrac{I\omega^2_1}{2}+\cfrac{mu^2}{2}\\
L=mvl=I\omega_1
\end{cases}
$$

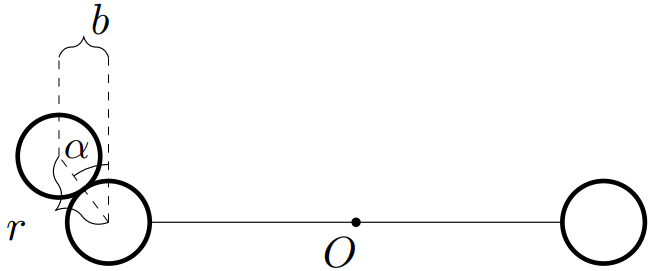
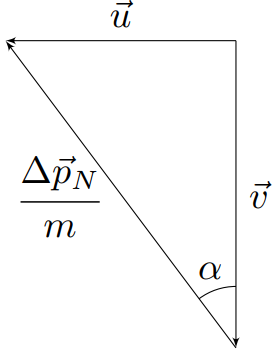
Подставляя значение $u$ систему уравнений из законов сохранения, получим:
$$v^2=\cfrac{I\omega^2_1}{m}+u^2=\cfrac{I}{m}\left(\cfrac{mvl}{I}\right)^2+v^2\tan^2\alpha\Rightarrow{\tan^2\alpha=1-\cfrac{ml^2}{I}}
$$
Учитывая, что $\sin\alpha=\frac{\tan\alpha}{\sqrt{1+\tan^2\alpha}}$, находим:

B2  ^1.00 Выразите угловую скорость $\omega_{i+1}$ системы после столкновения с $i+1$-ым вылетевшим шариком через $\omega_i$, $v$, $l$ и $k$.

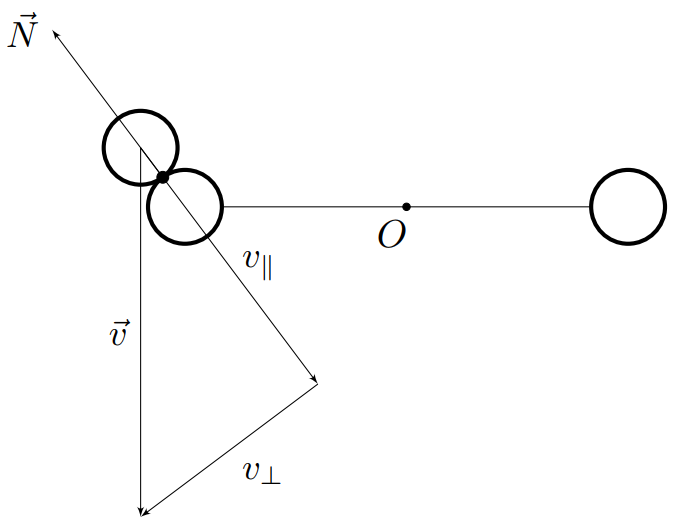
Скорость шарика сразу после удара также разложим на $u_\parallel$ и $u_\perp$. Их направления выберем теми же, что и у $v_\parallel$ и $v_\perp$ соответственно.
Запишем законы сохранения энергии и момента импульса относительно оси вращения:
$$\begin{cases}
E=\cfrac{I\omega^2_i}{2}+\cfrac{m(v^2_\parallel+v^2_\perp)}{2}=\cfrac{I\omega^2_{i+1}}{2}+\cfrac{m(u^2_\parallel+u^2_\perp)}{2}\\
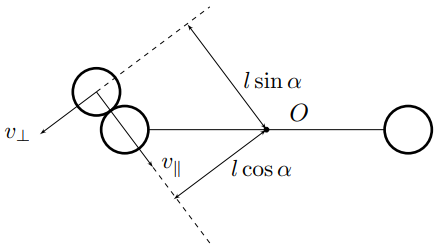
L=I\omega_i+mv_\parallel l\cos\alpha+mv_\perp l\sin\alpha=I\omega_{i+1}+mu_\parallel l\cos\alpha+mu_\perp l\sin\alpha
\end{cases}
$$
Поскольку $v_\perp=u_\perp$, а $v_\parallel=v\cos\alpha$, перепишем систему более компактно:
$$\begin{cases}
I\omega^2_i+mv^2\cos^2\alpha=I\omega^2_{i+1}+mu^2_\parallel\\
I\omega_i+mvl\cos^2\alpha=I\omega_{i+1}+mu_{\parallel}l\cos\alpha
\end{cases}
$$
Исключим из системы $u_\parallel$:
$$u^2_\parallel=v^2\cos^2\alpha-\cfrac{I(\omega^2_{i+1}-\omega^2_i)}{m}=\left(v\cos\alpha-\cfrac{I(\omega_{i+1}-\omega_i)}{ml\cos\alpha}\right)^2
$$
Раскрывая скобки и сокращая множитель $\omega_{i+1}-\omega_i$, получим:
$$\cfrac{2v}{l}=\omega_{i+1}\left(1+\cfrac{I}{ml^2\cos^2\alpha}\right)-\omega_i\left(\cfrac{I}{ml^2\cos^2\alpha}-1\right)
$$

B3  ^0.20 Чему равна $\omega_1$? Ответ выразите через $v_0$, $l$ и $k$.

Поскольку $\omega_0=0$, находим:

B4  ^0.80 Решив рекуррентное уравнение, полученное в пункте $\bf B2$, получите явное выражение для $\omega_i$. Ответ выразите через $i$, $v$ и $l$.

Вновь введём переменную $\omega'_i=\omega_i-v/l$ и получим:
$$\omega'_{i+1}\left(1+\cfrac{I}{ml^2\cos^2\alpha}\right)=\omega'_i\left(\cfrac{I}{ml^2\cos^2\alpha}-1\right)
$$
откуда после подстановки $I$:
$$\omega'_{i+1}=\omega'_i\left(\cfrac{7+3k^2}{13-3k^2}\right)\Rightarrow \omega'_i=\omega'_1\left(\cfrac{7+3k^2}{13-3k^2}\right)^{i-1}
$$
Для $\omega'_1$ имеем:
$$\omega'_1=\omega_1-\cfrac{v}{l}=-\cfrac{v(7+3k^2)}{l(13-3k^2)}
$$
Таким образом:
$$\omega'_i=\cfrac{v}{l}\left(\cfrac{7+3k^2}{13-3k^2}\right)^i
$$
и окончательно:

C1  ^0.50 Найдите, при каких значениях параметра $\alpha$ система в режиме сухого трения будет продолжать движение неограниченно долго после первого столкновения с шариком.

Для удобства решения найдём сначала угловую скорость системы $\omega^\uparrow$ после первого столкновения с шариком. Подставляя $\omega_i=0$ и $\omega_{i+1}=\omega^\uparrow$ в рекуррентное уравнение, получим:\[\omega^\uparrow=\frac{2\varepsilon\omega_0}{1+\varepsilon}.\]Временные зависимости $\omega(t)$ для режимов вязкого трения можно найти, как в решении к пунктам C5 и C7.

 

Случай сухого трения.

 

Кинетическая энергия вращательного движения системы должна быть потерь на трение за половину оборота, т.е.:\[\frac I2\omega^{\uparrow\,2} > \pi\alpha I\implies \alpha < \frac{\omega^{\uparrow\,2}}{2\pi}=\frac{2\varepsilon^2\omega_0^2}{\pi(1+\varepsilon)^2}.\]

C2  ^0.50 Найдите, при каких значениях параметра $\beta$ система в режиме линейного вязкого трения будет продолжать движение неограниченно долго после первого столкновения с шариком.

Случай линейного вязкого трения.

 

Поскольку $\omega(t)=\omega^\uparrow e^{-\beta T}$, то предельный угол поворота системы после первого соударения составит:\[\varphi=\int_0^{+\infty}\omega^\uparrow e^{-\beta t}~\mathrm dt=\frac{\omega^\uparrow}\beta.\]Этот угол должен быть больше $\pi$, поэтому:\[\beta < \frac{\omega^\uparrow}{\pi}=\frac{2\varepsilon\omega_0}{\pi(1+\varepsilon)}\]

C3  ^0.50 Найдите, при каких значениях параметра $\gamma$ система в режиме квадратичного вязкого трения будет продолжать движение неограниченно долго после первого столкновения с шариком.

Случай квадратичного вязкого трения.

 

Поскольку интеграл вида $\int\frac1x~\mathrm dx$ расходится при $x\to+\infty$, то при любом значении $\gamma$ система сможет совершить один оборот за конечное, пусть и экспоненциально большое время. Таким образом, $\gamma$ может быть произвольной положительной величиной.

Примечание: Так как в действительности в пределе малых угловых скоростей вязкое трение переходит в линейный режим, то реально значение $\gamma$ имеет верхний предел, однако этим мы здесь пренебрегаем.

C4  ^0.70 Найдите установившуюся среднюю по периоду угловую скорость системы $\overline\omega_1$ в режиме сухого трения. Выразите ответ через $\varepsilon$, $\alpha$ и $\omega_0$.

Приравнивая изменение кинетической энергии системы за один оборот к потерям на трение, имеем:\[\frac I2\omega^{\uparrow\,2}-\frac I2\omega^{\downarrow\,2}=\pi\alpha I\implies\omega^{\uparrow\,2}-\omega^{\downarrow\,2}=2\pi\alpha.\]Поскольку в режиме сухого трения движение системы происходит в постоянным угловым ускорением, средняя угловая скорость $\overline\omega$ будет равна среднему арифметическому $\omega^\uparrow$ и $\omega^\downarrow$. Для удобства введём ещё одну величину:\[\Delta\omega=\frac{\omega^\uparrow-\omega^\downarrow}2,\]тогда, добавив рекуррентное уравнение, получим следующую систему:\[\left\{\begin{array}l\overline\omega\Delta\omega=\frac{\pi\alpha}2\\\overline\omega+\cfrac{\Delta\omega}\varepsilon=\omega_0\end{array}\right.\implies\overline\omega^2-\omega_0\overline\omega+\frac{\pi\alpha}{2\varepsilon}=0.\]Это – квадратное уравнение, корни которого:\[\overline\omega_\pm=\frac{\omega_0\pm\sqrt{\omega_0^2-\cfrac{2\pi\alpha}\varepsilon}}{2}.\]Из физических соображений ясно, что необходимо взять бóльший корень $\overline\omega_+$. Итак:

C5  ^0.50 Найдите стационарное значение угловой скорости $\omega^\uparrow_2$ системы непосредственно после очередного столкновения с шариком в режиме линейного вязкого трения.

Случай линейного вязкого трения.

 

Уравнение на угловую скорость между столкновениями с шариком запишется в виде:\[\dot\omega=-\beta\omega.\]Его решение с начальным условием $\omega(t=0)=\omega^\uparrow$ имеет вид:\[\frac{\mathrm d\omega}\omega=-\beta~\mathrm dt\implies \omega=Ce^{-\beta t},~\omega(t=0)=C=\omega^\uparrow\implies\omega(t)=\omega^\uparrow e^{-\beta t}.\]Тогда время $T$ следующего столкновения с шариком определится из условия:\[\pi=\int_0^T\omega(t)~\mathrm dt=\int_0^T\omega^\uparrow e^{-\beta t}~\mathrm dt=\frac1\beta\left(1-e^{-\beta T}\right)\omega^\uparrow.\]Так как угловая скорость системы $\omega^\downarrow$ непосредственно перед столкновением с шариком равна:\[\omega^\downarrow=\omega^\uparrow e^{-\beta T},\]то имеем в итоге:\[\omega^\uparrow-\omega^\downarrow=\pi\beta.\]Подставляя это в рекуррентное уравнение, получим:\[\omega^\uparrow\left(1+\varepsilon^{-1}\right)+\left(\omega^\uparrow-\pi\beta\right)\left(1-\varepsilon^{-1}\right)=2\omega_0\implies\omega^\uparrow=\omega_0-\frac{\pi\beta}2\left(\varepsilon^{-1}-1\right).\]

C6  ^0.40 Найдите установившуюся среднюю по периоду угловую скорость системы $\overline\omega_2$ в режиме линейного вязкого трения.

Из результатов, полученных в предыдущем пункте, точное значение средней угловой скорости равно:\[\overline\omega_2=\frac{\pi}T=\frac{\pi\beta}{-\ln\left(1-\frac{\pi\beta}{\omega^\uparrow}\right)}=\frac{\pi\beta}{\ln\left(2\varepsilon\omega_0-\pi\beta(1-\varepsilon)\right)-\ln\left(2\varepsilon\omega_0-\pi\beta(1+\varepsilon)\right)}.\]

C7  ^0.50 Найдите стационарное значение угловой скорости $\omega^\uparrow_3$ системы непосредственно после очередного столкновения с шариком в режиме квадратичного вязкого трения.

Случай квадратичного вязкого трения.

 

Уравнение на угловую скорость между столкновениями с шариком запишется в виде:\[\dot\omega=-\gamma\omega^2.\]Его решение с начальным условием $\omega(t=0)=\omega^\uparrow$ имеет вид:\[\frac{\mathrm d\omega}{\omega^2}=-\gamma~\mathrm dt\implies\frac1\omega=\gamma t+C,~\omega(t=0)=\frac1C=\omega^\uparrow\implies\omega(t)=\frac1{\gamma t+\frac1{\omega^\uparrow}}=\frac{\omega^\uparrow}{1+\gamma\omega^\uparrow t}.\]Тогда время $T$ следующего столкновения с шариком определится из условия:\[\pi=\int_0^T\omega(t)~\mathrm dt=\int_0^T\frac{\omega^\uparrow}{1+\gamma\omega^\uparrow t}~\mathrm dt=\frac1\gamma\ln\left(1+\gamma\omega^\uparrow T\right)\implies T=\frac{e^{\pi\gamma}-1}{\gamma\omega^\uparrow}.\]Угловая скорость системы $\omega^\downarrow$ непосредственно перед столкновением с шариком составит:\[\omega^\downarrow=\omega(T)=\omega^\uparrow e^{-\pi\gamma}.\]Подставляя это в рекуррентное уравнение, имеем:\[\omega^\uparrow\left(1+\varepsilon^{-1}\right)+\omega^\uparrow e^{-\pi\gamma}\left(1-\varepsilon^{-1}\right)=2\omega_0\implies\omega^\uparrow=\frac{2\omega_0\varepsilon}{1-e^{-\pi\gamma}+\varepsilon\left(1+e^{-\pi\gamma}\right)}.\]

C8  ^0.40 Найдите установившуюся среднюю по периоду угловую скорость системы $\overline\omega_3$ в режиме квадратичного вязкого трения.

Из результатов, полученных в предыдущем пункте, точное значение средней угловой скорости равно:\[\overline\omega_3=\frac{\pi}T=\frac{\pi\gamma\omega^\uparrow}{e^{\pi\gamma}-1}=\frac{\pi\varepsilon\gamma\omega_0}{2\operatorname{sh}\frac{\pi\gamma}2\left(\operatorname{sh}\frac{\pi\gamma}2+\varepsilon\operatorname{ch}\frac{\pi\gamma}2\right)}.\]