

ОБОРУДОВАНИЕ:
ИЗВЕСТНЫЕ КОНСТАНТЫ:
Введём обозначения для параметров установки и будем их придерживаться в течение всей работы.
Не переобозначайте величины, упомянутые в условии!
ОБОЗНАЧЕНИЯ:
УКАЗАНИЯ:
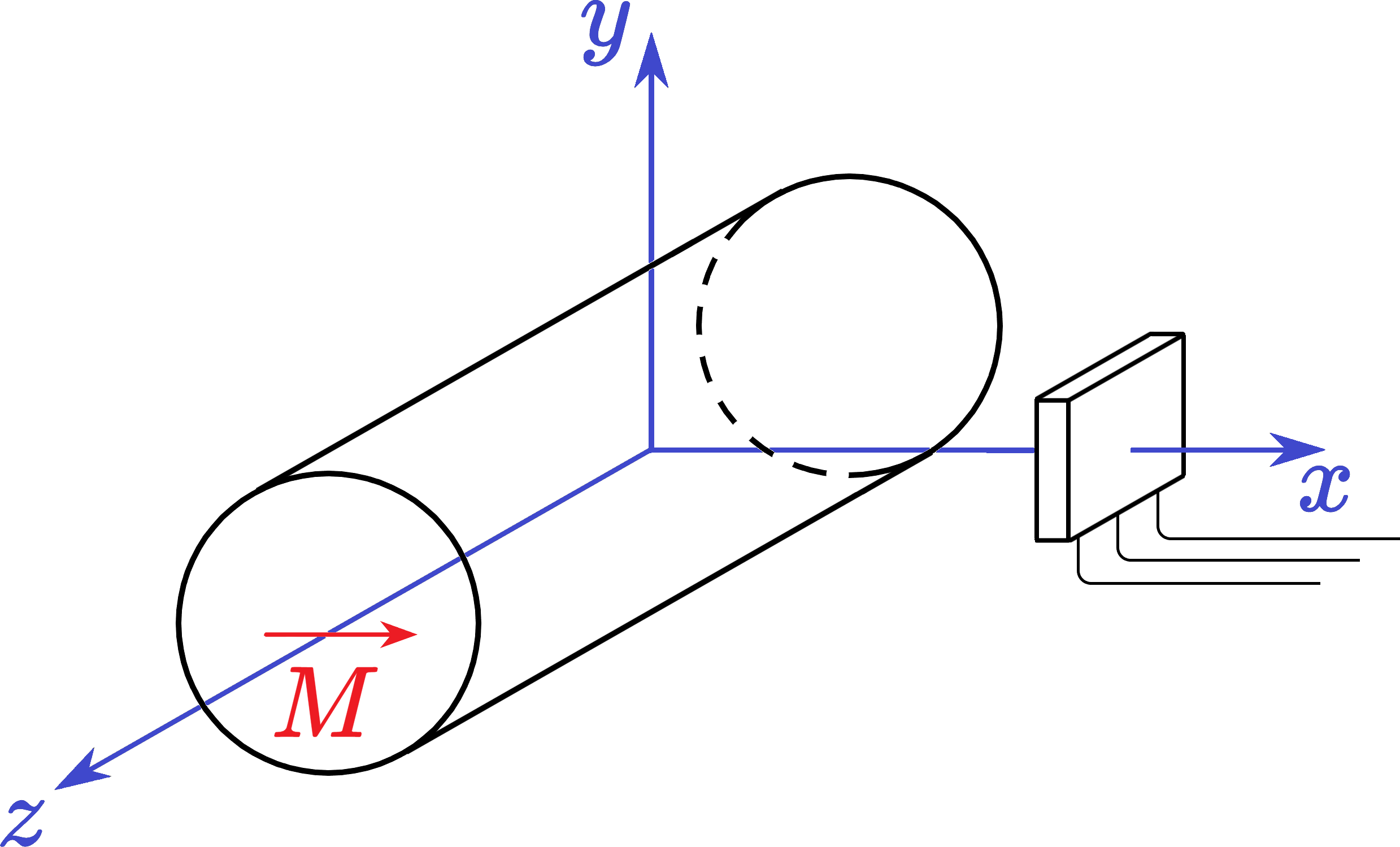
ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ ДАТЧИКА ХОЛЛА:

A1
2.00
Снимите зависимость $B(x)$. Проведите измерения в точках на оси $Ox$ во всем диапазоне $15~\text{мм} \leq x \leq 100~\text{мм}$. Для закрепления магнита на столе в удобном положении можно использовать опоры от подставки и клейкую массу. Пересчет напряжения в индукцию поля в этом пункте не требуется.
В пределе $x \to \infty$ (т.е. в «дальнем поле») магнитное поле $B(x)$ совпадает с полем точечного магнитного диполя, однако при небольших $x$ (в «ближнем поле») справедлива другая зависимость, в которой $n$ — неизвестное положительное число:
\begin{cases}
B(x) \propto 1/x^n, & x \sim 1~\text{см} \quad \text{ближнее поле}\\
B(x) \propto 1/x^3, & x \to \infty \quad \text{дальнее поле}
\end{cases}

Это можно сделать удобно и безопасно, если выполнить следующую последовательность действий:
Установите подставку с магнитами на наклоняемый столик. Регулировочными винтами добейтесь горизонтальности его поверхности, контролируя ее с помощью пузырькового уровня.
Подготовьте по одному отрезку длины $\approx10~\text{мм}$ грифелей каждого диаметра $d$. С помощью пинцета аккуратно положите любой из них в «желоб» между магнитами. Пронаблюдайте «левитацию», ее устойчивость, затухание различных видов колебаний. Проверьте, что колебания происходят вблизи середины магнитов, и если это не выполняется и грифель «уезжает» в сторону одной из опор, подкорректируйте наклон столика. Когда грифель остановится в положении равновесия, по шкале на одной из опор можно определить глубину $h$ (в миллиметрах), на которую он погружен относительно верхних точек магнитов. Будьте внимательны и хорошо подумайте, к какой линии шкалы относится подпись «-3».
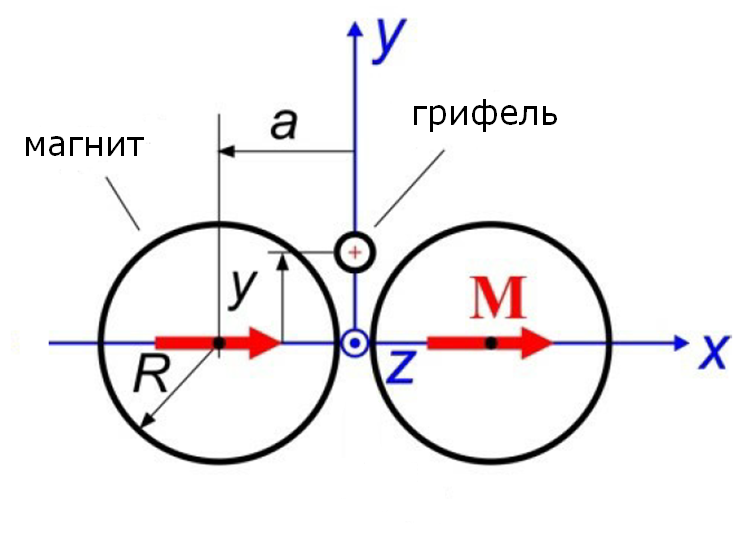
В зазоре между магнитами во всех точках на оси $Oy$ (см. рис.) магнитное поле направлено вдоль оси $Ox$ и задаётся некоторой функцией $B(y)$.
Считайте известным, что в однородном магнитном поле $B$ у цилиндра (графитового грифеля) появляется намагниченность $M_\text{гр}=\cfrac{2}{\mu_0} \cfrac{\chi}{\chi + 2} B$. Поле магнитов в области нахождения грифеля можно считать однородным.
Энергию грифеля, который в магнитном поле приобрел магнитный момент $\vec{m}_\text{гр}$, можно вычислить как $U=-\cfrac{1}{2}\left( \vec{m}_\text{гр} \cdot \vec B \right)$.
Далее считайте известным явный вид функции $ B(y) = \cfrac{\mu_0 M R^2}{a^2} \cdot \cfrac{1-u^2}{\left( 1+u^2 \right) ^2}$, где $u=\cfrac{y}{a}$.
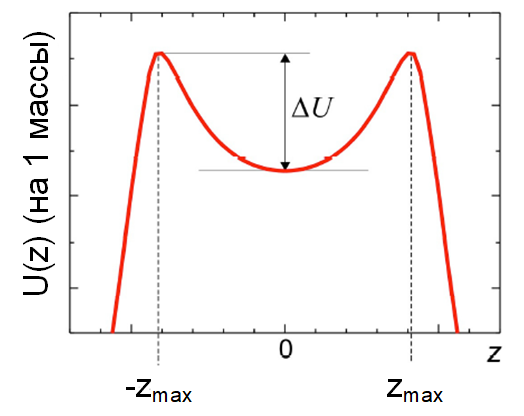
Используйте грифель с параметрами $d=0.5~\text{мм}$, $l\approx10~\text{мм}$. Вы можете наблюдать колебания грифеля вдоль «желоба» между магнитами, т.е. вдоль оси $Oz$.
Регулировочными винтами изменяйте наклон столика к горизонту $\alpha$ так, чтобы приподнимать один из концов «желоба» между магнитами. Пронаблюдайте, как при этом смещается положение равновесия $z_0$ горизонтальных колебаний грифеля.
Примечание: Обратите внимание, что пузырьковый уровень не подходит для точного измерения углов. Угол наклона столика следует рассчитывать по высоте его края, измеренной линейкой.
C3
1.50
В строго горизонтальном положении столика (убедитесь по положению равновесия грифеля) измерьте зависимость $T(l)$ периода колебаний от длины грифеля в максимально возможном диапазоне длин $l$. Получите не менее 10 экспериментальных точек $T(l)$. График строить в этом пункте не требуется.
Запишите критические длины $l_{min}$ и $l_{max}$, при которых меняется характер наблюдаемых процессов, и опишите происходящее.
Двугорбый потенциал (в расчете на единицу массы) можно аппроксимировать многочленом 4-й степени: $U(z) \approx c_0 + c_2 z^2 + c_4 z^4$.
Затухание горизонтальных колебаний грифеля обусловлено вязкостью воздуха и токами Фуко, возникающими при его движении в неоднородном магнитном поле и взаимодействующими с этим полем. С учетом названных двух эффектов можно записать силу сопротивления движению (в расчете на единицу массы) как $F_\text{сопр}/m=-\gamma \dot z$.
В этой части используйте грифель с параметрами $d=0.5~\text{мм}$, $l\approx10~\text{мм}$.