A1  ^2.00 Снимите зависимость $B(x)$. Проведите измерения в точках на оси $Ox$ во всем диапазоне $15~\text{мм} \leq x \leq 100~\text{мм}$. Для закрепления магнита на столе в удобном положении можно использовать опоры от подставки и клейкую массу. Пересчет напряжения в индукцию поля в этом пункте не требуется.

Закрепим магнит в подставках и зафиксируем их на столе с помощью клейкой массы. Расположим датчик на столе на высоте магнита на некотором расстоянии от него. Поворачивая магнит вокруг своей оси, добьемся максимальных показаний вольтметра. Это будет гарантировать правильную ориентацию оси $Ox$ и ее прохождение через датчик. Снимем зависимость $U(x)$.

A2  ^0.60 Запишите точную формулу $B(x)$ для точечного магнитного диполя.

Общая формула $\vec B \left(\vec r \right) = \cfrac{\mu_0}{4\pi}\cfrac{3(\vec m \cdot \vec r)\vec r - \vec m r^2}{r^5}$ в случае $\vec m \upuparrows \vec r$ упрощается до вида $B(x)=\cfrac{\mu_0}{4\pi}\cfrac{2m}{x^3}$.

A3  ^1.00 Постройте график $(-\ln B)$ от $\ln x$ для всего диапазона измеренных значений. При каком характерном $x_{crit}$ сменяется характер зависимости?

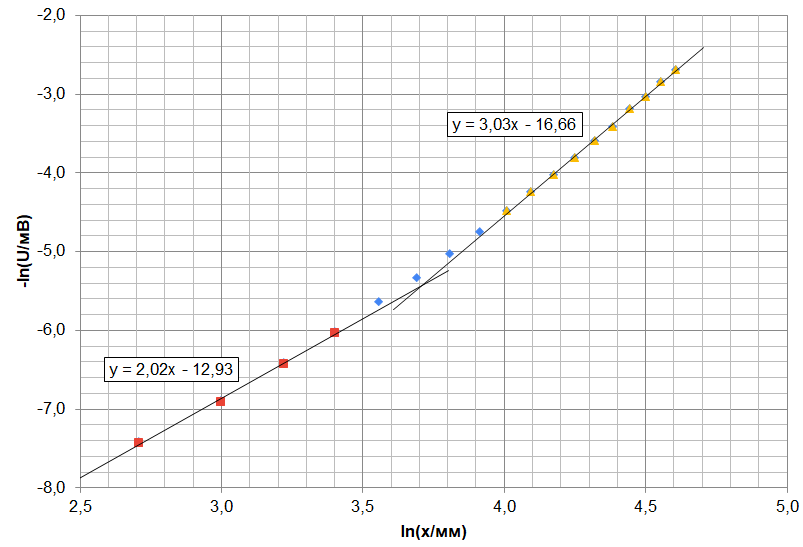
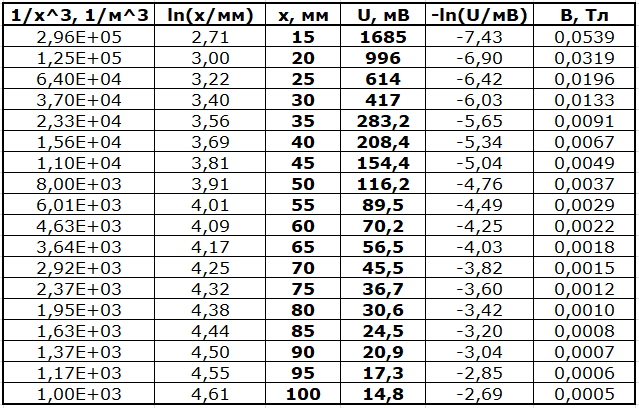
Точки графика, соответствующие $x \in [15; 30]~\text{мм}$, хорошо ложатся на прямую с коэффициентом наклона $n = 2.02 \approx 2$, точки при $x\in [55;100]~\text{мм}$ — на прямую с коэффициентом наклона $3.03 \approx 3$, как для точечного диполя. Характер зависимости меняется в окрестности $x_{crit}\approx 35~\text{мм}$.

A4  ^0.40 По построенному в пункте A3 графику определите величину $n$.

A5  ^1.00 Постройте линеаризованный график в таких координатах, чтобы по наклону графика определить намагниченность $M$ магнита (магнитный момент единицы объема). Рассчитайте численное значение величины $M$.

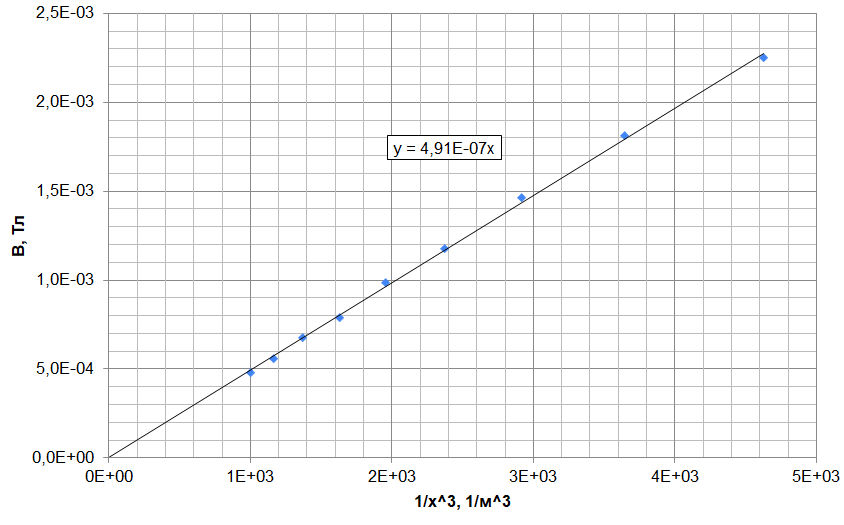
Используя чувствительность датчика $k = 31.25~\text{В}/\text{Тл}$, рассчитаем значения поля $B$. Построим график при больших $x\geq60~\text{мм}$, где на предыдущем графике видно, что точки хорошо ложатся на вторую прямую. Коэффициент наклона $\beta$ графика $B$ от $1/x^3$, исходя из теоретической формулы, равен $\beta= \cfrac{\mu_0 m}{2\pi} = \cfrac{\mu_0 \pi R^2 L}{2\pi} = \cfrac{\mu_0 MR^2 L}{2}$. По графику определяем $\beta=4.91 \cdot 10^{-7}$, откуда $M=\cfrac{2\beta}{\mu_0 R^2 L}=7.81\cdot10^5~\text{А}/\text{м}$.

B1  ^1.00 Измерьте зависимость $h(d)$. Укажите погрешности измерений, учитывая, что точность изготовления каждого грифеля $\Delta d = \pm 0.05~\text{мм}$. Опишите вид зависимости $h(d)$. Строить график не требуется.

Измерения $h$ для всех четырех доступных $d$ дают одинаковый результат, определяемый очень грубо из-за большой относительной погрешности: $h(d)=(2.5 \pm 0.5)~\text{мм}$. В пределах точности измерений зависимость от $d$ отсутствует.

Для иллюстрации того, что $h$ не зависит от $d$, можем уложить в «желоб» несколько разных грифелей друг за другом и убедиться, что они выстраиваются в одну линию.

B2  ^0.50 В листе ответов отметьте, каким материалом является графит, в соответствии с наблюдаемыми эффектами: диамагнитным, парамагнитным или ферромагнитным. Объясните ваш выбор.

Грифель намагничивается в поле магнитов и отталкивается от них, стремясь переместиться в положение с меньшим значением поля магнитов $B$. Значит, графит - диамагнетик.

B3  ^1.00 Выразите вертикальную силу $F(y)$, действующую на намагнитившийся грифель со стороны магнитного поля, через функцию $B(y)$ и величины $\chi$, $\mu_0$, $r$ и $l$. Выражение, содержащее другие величины, не будет засчитываться.

$F = -\cfrac{dU}{dy} = -\cfrac{d \left( -\cfrac{1}{2}(\vec m \cdot \vec B) \right)}{dy} = \cfrac{1}{2} \cfrac{2}{\mu_0} \cfrac{\chi}{\chi + 2} \pi r^2 l \cdot \cfrac{d}{dy} B^2 (y)$

B4  ^1.00 Получите окончательное выражение для $F(u)$ через величины $\chi$, $\mu_0$, $M$, $r$, $l$, $R$, $a$, $u$. Выражение, содержащее другие величины, не будет засчитываться.

Подставляем в полученную формулу $F(y)$ явный вид функции $ B(y) = \cfrac{\mu_0 M R^2}{a^2} \cdot \cfrac{1-u^2}{\left( 1+u^2 \right) ^2}$, где $u=\cfrac{y}{a}$. Для взятия производной удобно записать $ \cfrac{d}{dy} B^2 (y) = \cfrac{du}{dy} \cdot \cfrac{d}{du} B^2 (u) = \cfrac{1}{R} \cdot \cfrac{d}{du} B^2 (u) = \cfrac{1}{R} \cdot \cfrac{4u(1-u^2)(3-u^2)}{(1+u^2)^5}$. Приходим к окончательному ответу:

B5  ^0.50 Запишите, как выражается $u$ через измеренную величину $h$ и какое численное значение $u$ вы будете использовать в расчетах.

B6  ^1.00 Рассчитайте численно магнитную восприимчивость графита $\chi$ на основании измерений из части B1. Оцените погрешность результата методом границ.

В положении равновесия грифеля (при измеренном $h$) можно записать, что сумма сил вдоль вертикальной оси равна нулю:
$$F(u)-m_0g = -\cfrac{\chi}{\chi+2} \cfrac{\pi r^2l \mu_0 M^2R^4}{a^5} \cfrac{4u(1-u^2)(3-u^2)}{(1+u^2)^5} - m_0 g = 0,$$
где $m_0 = \rho \pi r^2 l$. Видно, что $r$ сокращается, поэтому теоретически подтверждается, что положение равновесия $h$, косвенно входящее в эту формулу, не зависит от диаметра грифеля $d$.

Подставляя $u=0.435$, $M=7.81\cdot10^5~\text{А}/\text{м}$ и приведенные в условии величины, получаем отрицательное численное значение $\chi=-2.6\cdot 10^{-4} < 0$, что соответствует диамагнитному материалу.

Для оценки погрешности можно воспользоваться методом границ и подставить $h_{min} = 2.0~\text{мм}$ и $h_{max}=3.0~\text{мм}$. С учетом значений $\chi$, получающихся при таких $h$, можно записать:

C1  ^1.00 Измерьте необходимые величины и получите зависимость $z_0(\alpha)$ для не менее 4 различных значений $\alpha$. График строить в этом пункте не требуется. Если обнаружится какая-то особенность поведения грифеля, запишите соответствующее $\alpha_{crit}$.

Будем наклонять столик, закручивая один из опорных винтов. Измерив высоту, на которой оказывается ближайший к этому винту край столика, найдем соответствующий наклон столика $\alpha=\cfrac{|h_{\alpha}-h_{\alpha=0}|}{\approx 20~\text{см}}$. По мере наклона столика положение равновесия грифеля постепенно смещается к расположенной ниже по склону опоре. При $\alpha_{crit}\approx0.0175~\text{радиан}$ положение равновесия исчезает, грифель перестает колебаться и упирается одним из концов в опору подставки для магнитов.

C2  ^1.00 Оцените численно значение величины $\Delta U$ и предъявите ваши рассуждения.

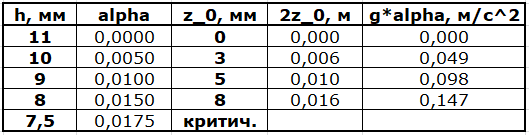
При наклоне $\alpha_{crit}$ разность удельных потенциальных энергий в магнитном поле между точками $z=0$ и, например, $z_0(\alpha_{crit})$, компенсируется разностью удельных потенциальных энергий в поле тяжести. В результате «провал» потенциала исчезает, положение равновесия более не существует, и грифель переходит в положение минимального суммарного потенциала — возле опоры. Таким образом, можно оценить $\Delta U \sim g\alpha_{crit}z_0(\alpha_{crit}) = 1.4~\text{мДж}/\text{кг}$, где $z_0(\alpha_{crit}$ - последнее измеренное положение равновесия перед улётом грифеля к опоре.

Более точная оценка — через вычисленную в пункте C4 величину $z_{max}=14~\text{мм}$ — положение «горба» потенциала: $\Delta U \sim g\alpha_{crit}z_{max} = 2.4~\text{мДж}/\text{кг}$.

C3  ^1.50 В строго горизонтальном положении столика (убедитесь по положению равновесия грифеля) измерьте зависимость $T(l)$ периода колебаний от длины грифеля в максимально возможном диапазоне длин $l$. Получите не менее 10 экспериментальных точек $T(l)$. График строить в этом пункте не требуется.

Запишите критические длины $l_{min}$ и $l_{max}$, при которых меняется характер наблюдаемых процессов, и опишите происходящее.

Для повышения точности определения $T$ будем измерять величину $NT$ - суммарное время $N$ колебаний. Разумно выбирать $N\sim10...20$, потому что при $N>20$ колебания практически незаметны из-за вякзости, и финальные колебания почти невозможно измерить.

C4  ^0.50 Оцените численно значение величины $z_{max}$ и предъявите ваши рассуждения.

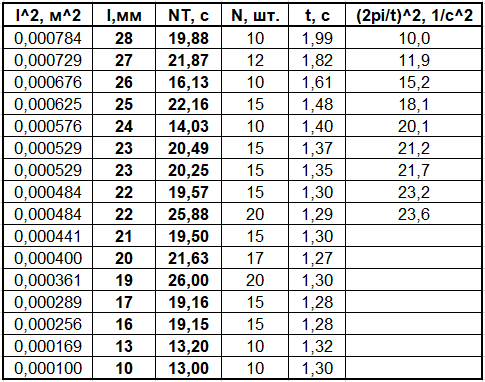
При длинах больше $l_{max} =28~\text{мм}$ положение устойчивого равновесия исчезает. Это происходит потому, что концы грифеля оказываются на участках очень резко убывающего потенциала магнитного поля, и при смещениях грифеля энергетически выгодным оказывается полный уход грифеля из положения равновесия в сторону одной из опор.

C5  ^1.00 Опираясь на измерения $z_0(\alpha)$, проведенные в части C1, постройте линеаризованный график и определите численное значение величины $c_2$.

Суммарная потенциальная энергия за счет магнитного и гравитационного полей равна $U_{\text{полн}}(z) \approx c_0+c_2z^2+g\alpha z$. Поправкой $c_4z^4$ здесь можно пренебречь, как уже обсуждалось ранее. Это пренебрежение оправдывается также линейностью получившегося линеаризованного графика.

Положение равновесия — минимум суммарной потенциальной энергии: $\cfrac{dU_{\text{полн}}}{dz} \Bigg|_{z_0} \approx 2c_2z_0 + g \alpha = 0$. Для линеаризации можно построить график $g \alpha$ от $2z_0$, тогда $c_2$ будет его коэффициентом наклона.

C6  ^1.00 Запишите закон сохранения энергии для колебаний грифеля длины $l$ в потенциале $U(z) = c_0 + c_2 z^2 + c_4 z^4$ и получите теоретическое выражение для периода $T(l)$ малых колебаний. Середина грифеля находится в точке с координатой $z=0$.

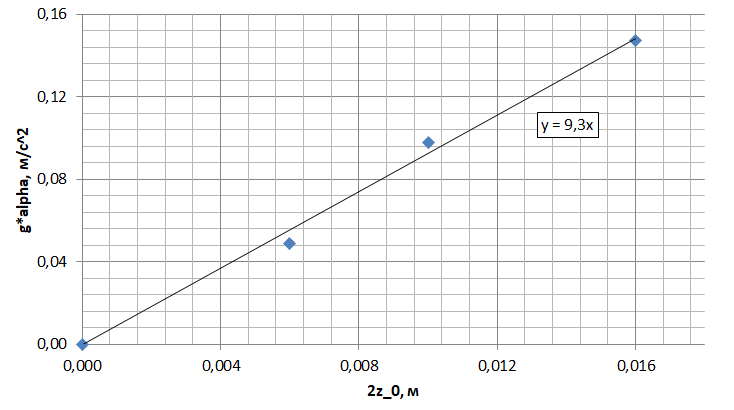
Пусть грифель смещен относительно положения равновесия на небольшое расстояние $\Delta z$. Изменение его потенциальной энергии в магнитном поле по сравнению с положением равновесия равно
$$\Delta W =
\rho \pi r^2 \Delta z \left(U\left(-\cfrac{l}{2}+\cfrac{\Delta z}{2}\right) - U\left(\cfrac{l}{2}+\cfrac{\Delta z}{2}\right) \right) =\rho \pi r^2 \Delta z \cdot \left( \cfrac{dU}{dz} \Bigg|_{z=l/2} \cdot \Delta z\right)=$$
$$= \rho \pi r^2 (\Delta z)^2 \cdot (2c_2z+4c_4z^3)\Big|_{z=l/2}=\cfrac{\rho \pi r^2 l (\Delta z)^2}{2}\cdot (2c_2+c_4l^2) $$.

Кинетическая энергия грифеля при этом равна $K=\cfrac{\rho \pi r^2 l \cdot \dot{(\Delta z)}^2}{2}$.

Из закона сохранения энергии следует $dW+dK=0$:
$$\cfrac{\rho \pi r^2 l\cdot 2(\Delta z) \dot{(\Delta z)}}{2}\cdot (2c_2+c_4l^2) + \cfrac{\rho \pi r^2 l \cdot 2\dot{(\Delta z)}\ddot{(\Delta z)}}{2}=0.$$
Это выражение можно сократить на $\rho \pi r^2 l\cdot \dot{(\Delta z)}$, останется:
$$\ddot{(\Delta z)}=-(2c_2+c_4l^2) \cdot (\Delta z).$$
Отсюда период колебаний:

C7  ^1.00 Опираясь на измерения $T(l)$, проведенные в части C3, постройте линеаризованный график и определите численные значения величин $c_2$ и $c_4$.

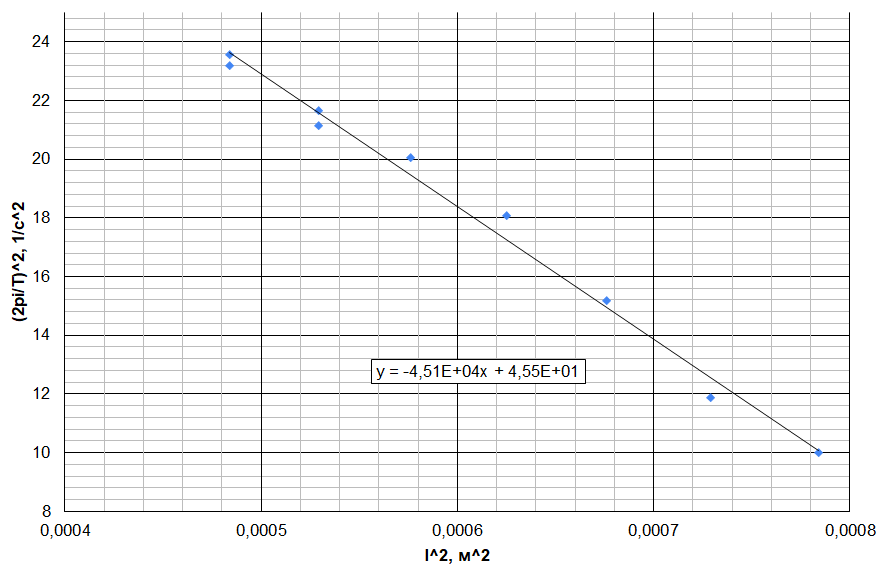
Для линеаризации зависимости при больших длинах $22~\text{мм} \leq l \leq28~\text{мм}$, где проявляется поправка $c_4 z^4$ и период существенно зависит от $l$, построим зависимость $\left( \cfrac{2\pi}{T} \right) ^2$ от $l^2$. Коэффициент наклона графика будет равен $c_4$, а свободный член $2c_2$.

D1  ^3.00 Проведите необходимые измерения затухающих колебаний, постройте линеаризованный график и рассчитайте численно значение величины $\gamma$.

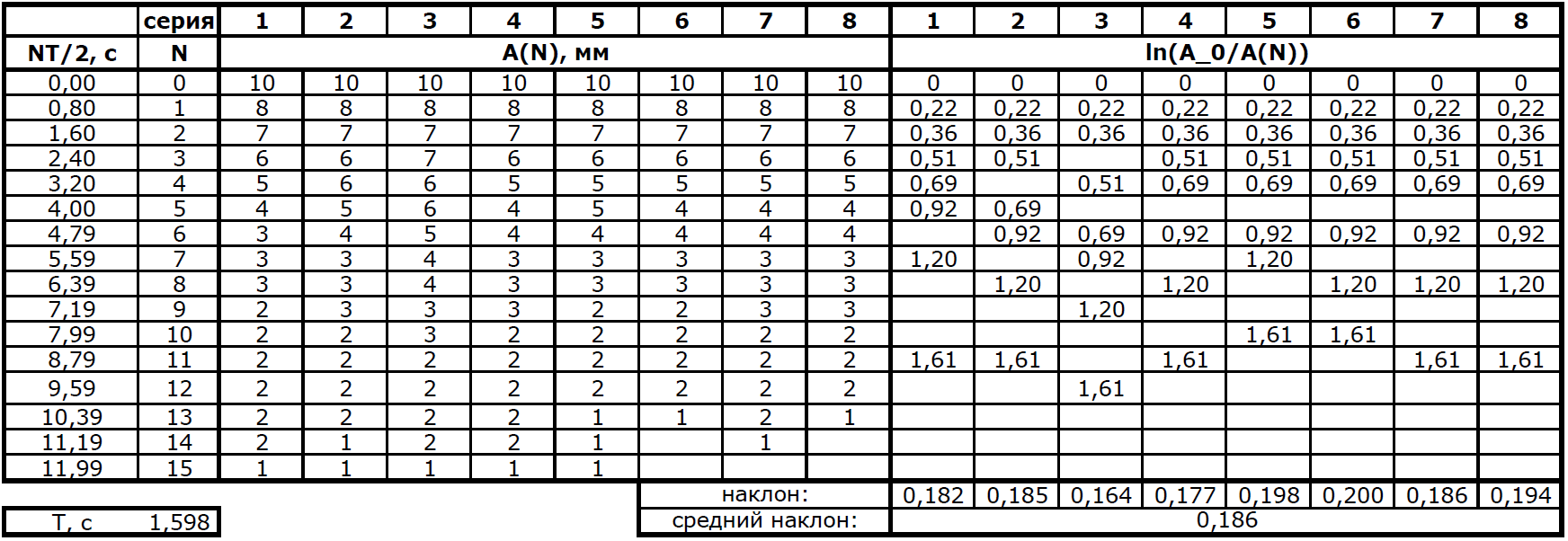
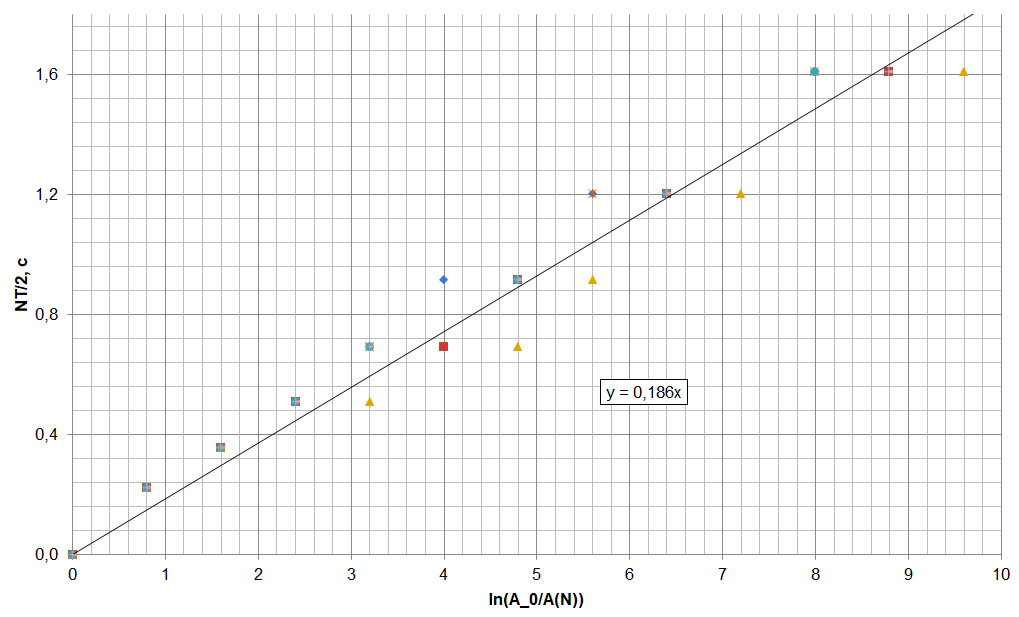
Если сила сопротивления определяется выражением $F_{\text{сопр}}/m = -\gamma \dot z$, то уравнение колебаний записывается в виде $\ddot z + \gamma \dot z + \omega_0^2 z = 0$. Решение этого уравнения — гармонические колебания с амплитудой, затухающей со временем как $A(t)=A_0 e^{-\cfrac{\gamma}{2}t}$. Амплитуда зависит от номера колебания: $A(N)=A_0 e^{-\cfrac{\gamma}{2}NT}$. Для линеаризации можно построить зависимость $\ln\left(\cfrac{A_0}{A(N)}\right)$ от $\cfrac{NT}{2}$, коэффициент ее наклона будет равен $\gamma$.

Измерим период колебаний, проведя несколько серий по 10...15 колебаний: $T=1.598~\text{с}$. Запустим затухающие колебания, отклонив грифель от положения равновесия. Будем записывать все последовательные значения амплитуды, наблюдая их по вставленному в зазор между магнитами фрагменту миллиметровки. Проведем несколько таких "запусков", нанося соответствующие серии точек на линеаризованный график. Если примерно одинаковые амплитуды были у разных номеров колебаний, то на графике отметим только средний из номеров.

Усредняя наклоны линейных графиков, получившихся для разных серий измерений, получаем среднее значение $\gamma \approx 0.19~1/\text{с}$.