Скрипящая дверь

Скрип очень распространен в повседневной жизни, и наблюдается при закрывании дверей, при письме мелом на доске, при игре на скрипке, при ходьбе в новой обуви и других явлениях. Здесь в Израиле, причины обуславливающие скрип, вызывают сильные землетрясения, повторяющиеся один раз в несколько десятилетий. Они происходят недалеко от Мертвого моря, чуть выше самого глубокого из известных разломов в земной коре.

Физический механизм скрипа кроется в различии между коэффициентом трения покоя и коэффициентом трения скольжения. В данной задаче мы изучим этот механизм применительно к открывающейся двери.

Часть А. Простейшая модель

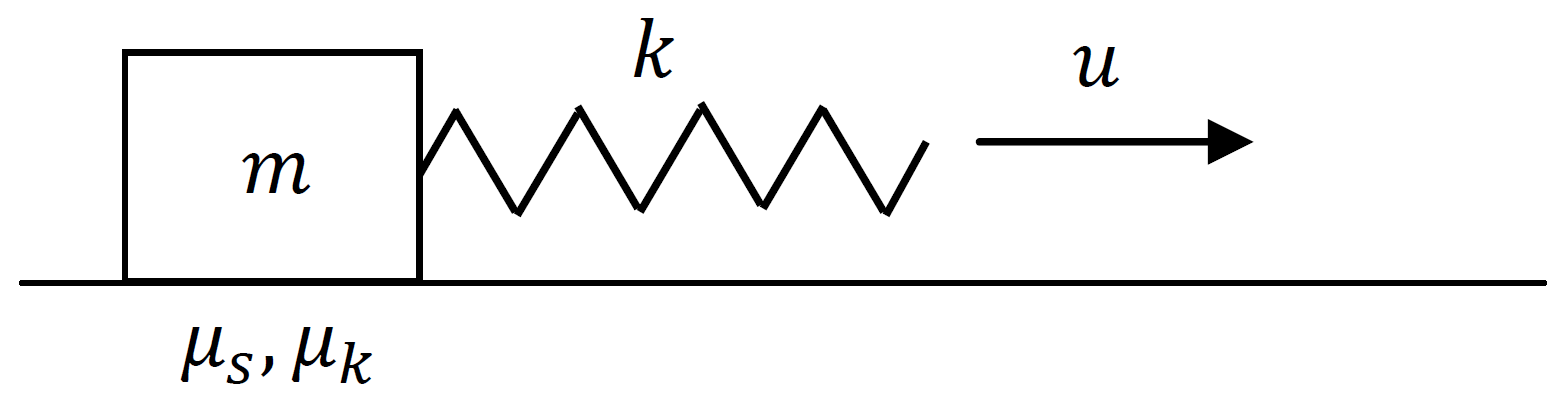
Рассмотрите следующую систему (см. рис. 1):
К телу массой $m$ присоединена длинная идеальная пружина с коэффициентом жесткости $k$, другой конец которой тянут с постоянной скоростью $u$. Коэффициент трения покоя и
коэффициент трения скольжения о поверхность равны $\mu_s$
и $\mu_k$, причем $\mu_k < \mu_s$.

Эта простейшая модель допускает два различных режима движения:

1. Движение всегда сопровождается проскальзыванием. Назовем этот режим чистым скольжением.
2.Движение, при котором происходит поочередная смена проскальзывания и покоя относительно поверхности. Это явление назовем прерывистым скольжением. Такое прерывистое скольжение является источником скрипящего звука, с которым мы часто сталкиваемся в повседневной жизни.

Рассмотрите случай, когда в начальный момент времени, $t = 0$, тело тянут по полу со скоростью $v_0$, и сила упругости пружины уравновешивается силой трения скольжения. Считайте, что $0 < v_0 < u$. При этом удлинение пружины будет периодически изменяться как функция времени $t$.

A1  ^0.60 Найдите период $T_0$ и амплитуду $A$ этих колебаний.

A2  ^0.40 Изобразите качественно график зависимости удлинения пружины от времени $x(t)$ в интервале $0 < t < 3T_0$.

A3  ^1.20 Рассмотрите другой случай, когда в начальный момент времени $t = 0$ тело находится в покое, а начальное удлинение пружины $x$, точно такое же, как в пунктах А1-А2. Изобразите качественный график зависимости скорости тела от времени $v(t)$ относительно поверхности в интервале $0 < t < 3T$, где $T$ - новый период колебаний $x(t)$. Движение направо соответствует положительному знаку скорости $v$. Укажите на вашем графике приблизительное положение горизонтальной линии $v = u$.

A4  ^0.50 Для начальных условий пункта A3, найдите среднее по времени значение удлинения пружины $\overline{x}$ за один период колебаний.

A5  ^2.40 Для условий пункта A3, найдите период $T$ колебаний $x(t)$.

Режим движения с прерывистым скольжением прекращается при достаточно больших значениях скорости $u$. Давайте рассмотрим один из возможных механизмов для объяснения этого явления.

A6  ^2.40 Будем считать, что за каждый период колебаний $T$ небольшое количество полной энергии колебаний рассеивается и переходит в тепло. Пусть $\eta = | \Delta A / A|$ есть относительная потеря амплитуды за один период при движении в режиме прерывистого скольжения. Полагая $\eta \ll 1$, найдите критическую скорость $u_c$, по достижении которой движение с \textbf{прерывистым скольжением} становится невозможным.

Затухание, рассмотренное в пункте A6, не надо учитывать во второй части этой задачи.

Часть B. Дверь со скрипом

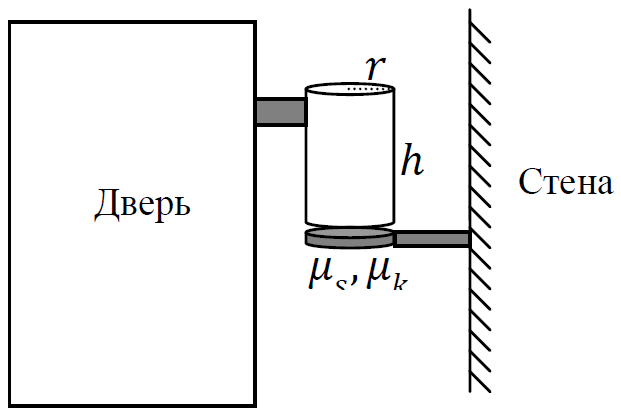
Дверная петля представляет собой полый, открытый металлический цилиндр радиуса $r$, высотой $h$ и толщиной стенок $\Delta r$. Нижнее основание цилиндра находится на металлической опоре, прикрепленной к стене (область контакта – это кольцо радиуса $r$ и толщиной $\Delta r \ll r$); см. рис. 2. Коэффициенты трения скольжения и трения покоя между цилиндром и его опорой равны соответственно $\mu_k$ и $\mu_s$, причем $\mu_k < \mu_s$. Верхнее основание цилиндра жестко прикреплено к двери, которая считается абсолютно твердым телом. Обычно дверь висит на двух или трех петлях, но ее вес падает только на одну петлю — ту, которая и будет скрипеть. Цилиндр этой петли давит на свою металлическую опору с силой, равной весу всей двери, масса которой $M$.

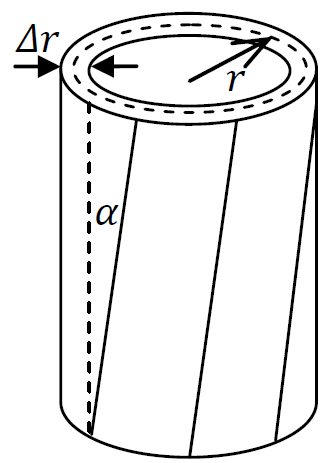
Цилиндр самой петли не является абсолютно твердым телом, он подвергается деформации сдвига без изменения своей формы, так что вертикальные линейные сегменты становятся наклонными с некоторым маленьким углом $\alpha$ (см. рисунок 3). Сила упругости, действующая на элемент малой площади $dS$ и обусловленная деформацией сдвига, определяется как:
\begin{equation*}
dF = G \alpha dS,
\end{equation*}где $G$ - модуль сдвига (константа, характеризующая упругие свойства материала). Для расчетов используйте следующие значения $r = 5 \,мм$, $h = 3 \,см$, $\Delta r = 1 \, мм$, $\mu_s = 0.75$, $\mu_k = 0.55$, $G = 8 \cdot 10^{10} \,Па$, $M = 30 \,кг$, $g = 9.8\, м/с^2$. Используйте приближение $\Delta r \ll r$.

B1  ^1.00 Дверь начинают очень медленно поворачивать из состояния покоя. Для маленьких углов поворота двери, получите выражение для коэффициента кручения $\kappa = \tau / \theta$, где $\tau$ –- вращающий момент, необходимый для поворота двери на угол $\theta$.

B2  ^1.50 При вращении двери с малой угловой скоростью происходит переход к режиму прерывистого трения, сопровождающийся испусканием звукового импульса — скрипа. Найдите угловую скорость $\Omega$ двери, при которой частота звука достигает слышимого диапазона с $f = 20$ Гц. Считайте, что частота звуковых колебаний $f_0$, возбуждаемых в стержне при самом скольжении велика, так что $f_0 \gg f$. Получите аналитический и численный результаты.