Исследование равновесия различных механических систем представляет собой важную технологическую задачу. Например, процесс «ходьбы» (чрезвычайно сложный!) совершенно естественен. Однако при разработке человекоподобных роботов основная сложность возникает в процессе поддержания равновесия конструкции при ходьбе. Вам предлагается рассмотреть одну из простейших моделей, которая демонстрирует динамическое состояние равновесия, — маятник Капицы.

Модель состоит из физического маятника, состоящего из тела, материальной точки, массы~$m$, соединенной с точкой опоры жестким невесомым стержнем длины~$l$, который свободно вращается вокруг оси. В свою очередь ось может совершать колебания в вертикальном направлении амплитуды $a\ll l$ и очень большой частоты~$\omega$, т.е. $y_0(t)=a\cos\omega t$. Возможная практическая реализация этого представлена на рисунке слева, обозначения приведены на рисунке справа (угол, который стержень составляет с вертикалью обозначим~$\varphi$). Ускорение свободного падения равно~$\vec g=-g\vec j$.

A1  ^0.50 Система имеет одну степень свободы, угол~$\varphi$, и положение маятника можно описать функцией этого угла. Выразите декартовы координаты тела $x(t)$ и $y(t)$ как функции угла $\varphi(t)$ и времени.

A2  ^0.50 Найдите компоненты скорости $v_x$ и $v_y$ тела. Ответ выразите через угловую скорость $\frac{d\varphi}{dt}$ и время.

A3  ^0.50 Найдите кинетическую и энергию тела. Ответ выразите через угол $\varphi$, угловую скорость $\frac{d\varphi}{dt}$ и время.

A4  ^1.00 Получите выражение для мгновенной мощности $N$ силы, прикладываемой к точке подвеса маятника. Ответ выразите через $m, g, l, a, \omega, \varphi, \frac{d\varphi}{dt}, \frac{d^2\varphi}{dt^2}$ и время.

A5  ^1.00 Покажите, что уравнение движения выглядит следующим образом:
$$
\cfrac{d^2\varphi}{dt^2}=-\cfrac{1}{l}(g-a~\omega^2\cos \omega t)\sin \varphi.
$$

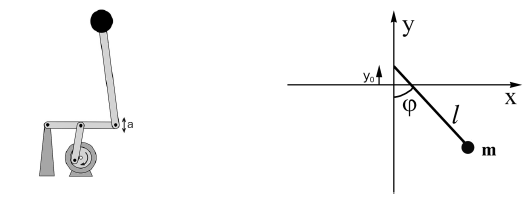
При определенных условиях для малых значений амплитуды~$a$ и больших значений частоты колебаний оси~$\omega$ решение уравнения из пункта A5 демонстрирует особое поведение: движение ведет себя как суперпозиция двух компонент: $\gamma$, которая медленно изменяется во времени и имеет большую амплитуду, и второй компоненты~$\beta$, которая быстро меняется со временем и имеет небольшую амплитуду.

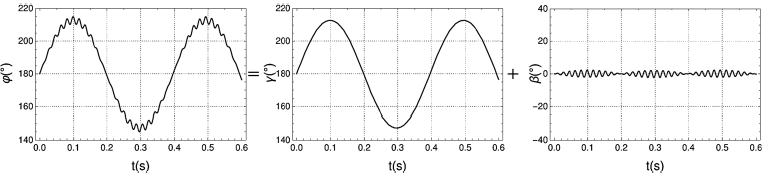
Таким образом можно разложить $\varphi=\gamma+\beta$, где $\gamma\gg\beta$ и значение медленной компоненты~$\gamma$ можно считать постоянным для достаточного числа периодов быстрой компоненты~$\beta$.

B1  ^1.00 Покажите, что выражение для быстрой компоненты~— $\beta=-\frac{a}{l}~\sin\gamma \cos\omega t$ (для произвольного значения~$\gamma$) является приближенным решением уравнения движения из пункта A5 при указанных выше условиях. Рассмотрите режим колебаний, в котором $g$ пренебрежимо мал по сравнению с $a\omega^2$, т.е. $a\omega^2\gg g$.

B2  ^2.50 Комбинируя уравнение движения из пункта A5 с разложением $\varphi=\gamma+\beta$ и с выражением из предыдущего пункта, найдите выражение для $\frac{d^2\gamma}{dt^2}$, которое описывает динамику медленной компоненты~$\gamma$ усредняя по большому количеству быстрых колебаний с частотой~$\omega$, пренебрегая только членами порядка $a^n$, где $n>2$. Выразите $\frac{d^2\gamma}{dt^2}$ через $g, a, \omega, l$ и $\gamma$. Упростите окончательное выражение, считая $l\omega^2\gg a\omega^2\gg g$.

Теперь перейдём в систему отсчета, связанную с точкой подвеса маятника. Во всех дальнейших пунктах все величины требуется найти в этой системе отсчета. Пренебрежения из пункта B2 справедливы здесь и в последующих пунктах задачи.

B3  ^0.70 Получите выражение для усредненного по времени момента всех сил $M_O$, действующих на маятник относительно точки подвеса. Ответ выразите через $m, g, l, a, \omega$ и $\gamma$.

B4  ^0.70 Назовем эффективным потенциалом скалярную функцию $V(\gamma)$, производная которой по углу $\gamma$ равняется усредненному моменту сил из предыдущего пункта, взятому со знаком минус. Получите выражение для эффективного потенциала $V(\gamma)$ с точностью до произвольной постоянной. Ответ выразите через $m, g, l, a, \omega$ и $\gamma$.

B5  ^1.00 Покажите, что для $(a\omega)^2>2gl$ этот потенциал имеет несколько минимумов: минимум при $\gamma=0$, который появляется в случае свободных колебаний маятника; дополнительный минимум $\gamma=\pi$. Покажите, что оба положения удовлетворяют условиям устойчивого равновесия.

B6  ^0.60 Найдите периоды колебаний $T_0$ и $T_\pi$ величины $\gamma$, соответствующие положениям из пункта B5.