Последние достижения в области нанотехнологий позволили создать «искусственные атомы», так называемые квантовые точки. Это нанометровые структуры, которые благодаря своим оптическим и электронным свойствам имеют разнообразные применения: от квантовых компьютеров, солнечных батарей до визуализации живых клеток. В этой задаче будет рассмотрена модель движения электронов в квантовой точке.

Рассмотрим движение двух электронов (массой $m$ и зарядом $q=-e$) в плоскости, перпендикулярной линиям однородного магнитного поля индукции $\vec B=B\vec k$. Электроны можно считать материальными точками, между которыми есть только кулоновское взаимодействие. Релятивистскими эффектами можно пренебречь.

Пусть в начальный момент электроны находятся на расстоянии $d$ друг от друга. Электронам сообщают одинаковые по модулю, но противоположные по направлению скорости, такие, что расстояние между ними не изменяется при дальнейшем движении.

A1  ^1.00 Каким может быть минимальное расстояние $d_\min$ между электронами, чтобы описанное выше движение было возможным?

A2  ^0.50 Найдите скорость $v_m$, которую нужно сообщить электронам, чтобы при их движении между ними сохранялось найденное в A1 расстояние $d_\min$.

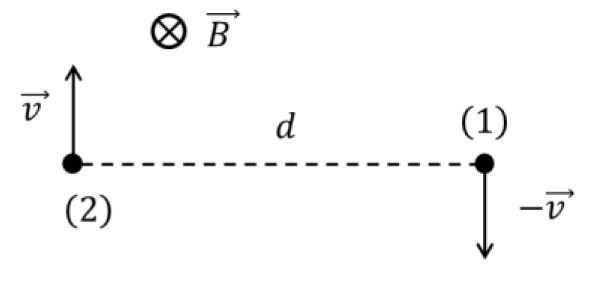
Рассмотрим теперь случай, когда только одному электрону сообщают в начальный момент времени скорость $v_0$, такую, что расстояние между ними не изменяется и остается равным $d_1=2\sqrt[3]{\cfrac{m}{4\pi\varepsilon_0 B^2}}$.

B1  ^0.50 Найдите угловую скорость центра масс $\omega$ во время движения электронов.

B2  ^1.00 Найдите время, через которое у обоих электронов сравняются абсолютные значения скорости в первый раз.

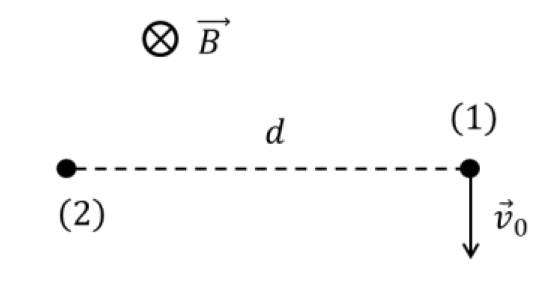
Вернемся к модели из части А. Электроны находятся на расстоянии $d$ друг от друга, и им сообщают противоположные скорости $v_0$.

C1  ^0.20 Получите выражение для кинетической энериии одного электрона $K=K(m, v_r, \omega, r)$, где $v_r=\cfrac{dr}{dt}, \omega=\cfrac{d\theta}{dt}$, а $r$ и $\theta$~— задают положение электрона в системе центра масс.

С2  ^0.80 Найдите, чему равна производная момента импульса по времени $\cfrac{dL}{dt}$ при движении электронов.

C3  ^0.50 Найдите интеграл движения для рассматриваемого случая, т.е. найдите такую функцию $J$, для которой справедливо $\cfrac{dJ}{dt}=0$.

C4  ^1.00 Выразите полную энергию электрона в виде $E=K(v_r)+U(r)$. Выразите ее через $J, e, B, r$ и физические постоянные.

C5  ^0.50 Схематично изобразите график зависимости $U(r)$, укажите его характерные особенности.

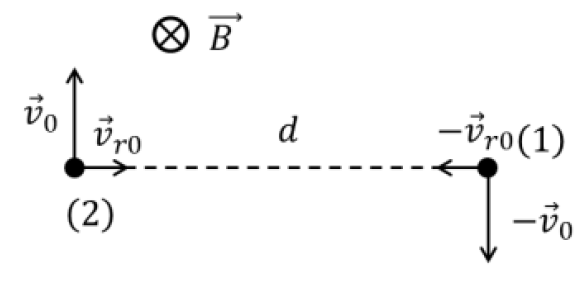
С6  ^1.00 Разложите функцию $U(r)$ в ряд Тейлора до первого нетривиального члена вблизи особых точек из пункта C5. Основываясь на разложении, схематично изобразите траекторию электронов, которым сообщили небольшую радиальную компоненту скорости $v_{r0}$ вдобавок к скорости движения по окружности $v_0$.