A1  ^1.00 Каким может быть минимальное расстояние $d_\min$ между электронами, чтобы описанное выше движение было возможным?

Запишем второй закон Ньютона в проекции на линию, проходящую через электроны. Поскольку расстояние не меняется, ускорение равно $\frac{v^2}{r}$. Получаем в итоге уравнение:
$$
\frac{2mv^2}{d}=vBe-\frac{e^2}{4\pi\varepsilon_0 d^2}
$$

Решаем квадратное уравнение относительно $v$. Дискриминант этого уравнения равен $(Be)^2-\frac{2me^2}{\pi\varepsilon_0d^3}$.

Из дискриминанта видно, что решения для скорости существуют только для $d\geqslant2\sqrt[3]{\frac{m}{4\pi\varepsilon_0 B^2}}$. Это и будет минимальное возможное расстояние.

A2  ^0.50 Найдите скорость $v_m$, которую нужно сообщить электронам, чтобы при их движении между ними сохранялось найденное в A1 расстояние $d_\min$.

Так как дискриминант равен нулю: $$v_m = -\frac{b}{2a}= \frac{Be}{2m}d_{\text{min}}=\frac{e}{2}\sqrt[3]{\frac{B}{4\pi\varepsilon_0m^2}}$$

B1  ^0.50 Найдите угловую скорость центра масс $\omega$ во время движения электронов.

Центр масс движется под действием двух сил Лоренца: $$m\vec{a} = \left[\vec{v}_1\times \vec B\right]q+\left[\vec{v}_2\times \vec B\right]q = \left[\left(\vec{v}_1+\vec{v}_2\right)\times \vec B\right]q = 2\left[\vec{v}_{CM}\times \vec B\right]q$$

Так как других внешних сил нет,скорость центра масс поворачивается, но не меняется по модулю. Ускорение центра масс в таком случае равно $\vec\omega\times\vec v$
$$2m\left[\vec\omega_{CM}\times\vec v\right] \equiv 2\left[\vec{v}_{CM}\times \vec B\right]q$$
$$\omega_{CM} = \frac{Be}{m}$$

B2  ^1.00 Найдите время, через которое у обоих электронов сравняются абсолютные значения скорости в первый раз.

При движении, описанном в условии, кинетическая энергия сохраняется. Таким образом угловая скорость относительно центра масс не меняется. $$\omega = \frac{v_0}{d_1}$$

Скорость центра масс и относительная скорость равны, поэтому скорости электронов сравняются, когда угол между скоростью центра масс и относительной скоростью станет равным $\frac{\pi}{2}$.
$$t = \frac{\pi}{2}\frac{1}{\left|\frac{v_0}{d_1} - \frac{eB}{m}\right|}$$

C1  ^0.20 Получите выражение для кинетической энериии одного электрона $K=K(m, v_r, \omega, r)$, где $v_r=\cfrac{dr}{dt}, \omega=\cfrac{d\theta}{dt}$, а $r$ и $\theta$~— задают положение электрона в системе центра масс.

$K=\frac{m}{2}(\omega^2r^2+v_r^2)$

С2  ^0.80 Найдите, чему равна производная момента импульса по времени $\cfrac{dL}{dt}$ при движении электронов.

Момент импульса меняется за счет составляющей силы Лоренца, отвечающей радиальной составляющей скорости.
$$\frac{dL}{dt} = v_rBer$$

C3  ^0.50 Найдите интеграл движения для рассматриваемого случая, т.е. найдите такую функцию $J$, для которой справедливо $\cfrac{dJ}{dt}=0$.

Интегрируя выражение для $\frac{dL}{dt}$ получаем интеграл движения
$$J = L-\frac{eBr^2}{2}$$

C4  ^1.00 Выразите полную энергию электрона в виде $E=K(v_r)+U(r)$. Выразите ее через $J, e, B, r$ и физические постоянные.

Выражаем угловую скорость через $J$, затем подставляем в выражение для кинетической энергии. $\omega = \frac{1}{m}\left(\frac{J}{r^2}+\frac{eB}{2}\right)$.

К кинетической энергии надо добавить энергию кулоновского взаимодействия, приходящуюся на один электрон. $$E = \frac{mv_r^2}{2}+\frac{r^2}{2m}\left(\frac{J}{r^2}+\frac{eB}{2}\right)^2+\frac{e^2}{16\pi\varepsilon_0r}$$

C5  ^0.50 Схематично изобразите график зависимости $U(r)$, укажите его характерные особенности.

Пределы $U(r)$ в точках $0$ и $+\infty$ равны $+\infty$, при этом функция непрерывна на отрезке $(0, +\infty)$

Вторая производная функции $U(r)$ имеет следующий вид:
$$\frac{Ar^4+Br+C}{r^4}; ~~A,~B,~C, ~r > 0$$
На интересующем нас отрезке она всегда больше нуля, оба предела бесконечные, следовательно есть минимум, причем единственный.

С6  ^1.00 Разложите функцию $U(r)$ в ряд Тейлора до первого нетривиального члена вблизи особых точек из пункта C5. Основываясь на разложении, схематично изобразите траекторию электронов, которым сообщили небольшую радиальную компоненту скорости $v_{r0}$ вдобавок к скорости движения по окружности $v_0$.

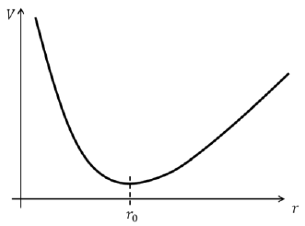
Так как мы будем оставаться в окрестности минимума, электроны будут совершать гармонические колебания вдоль радиуса.