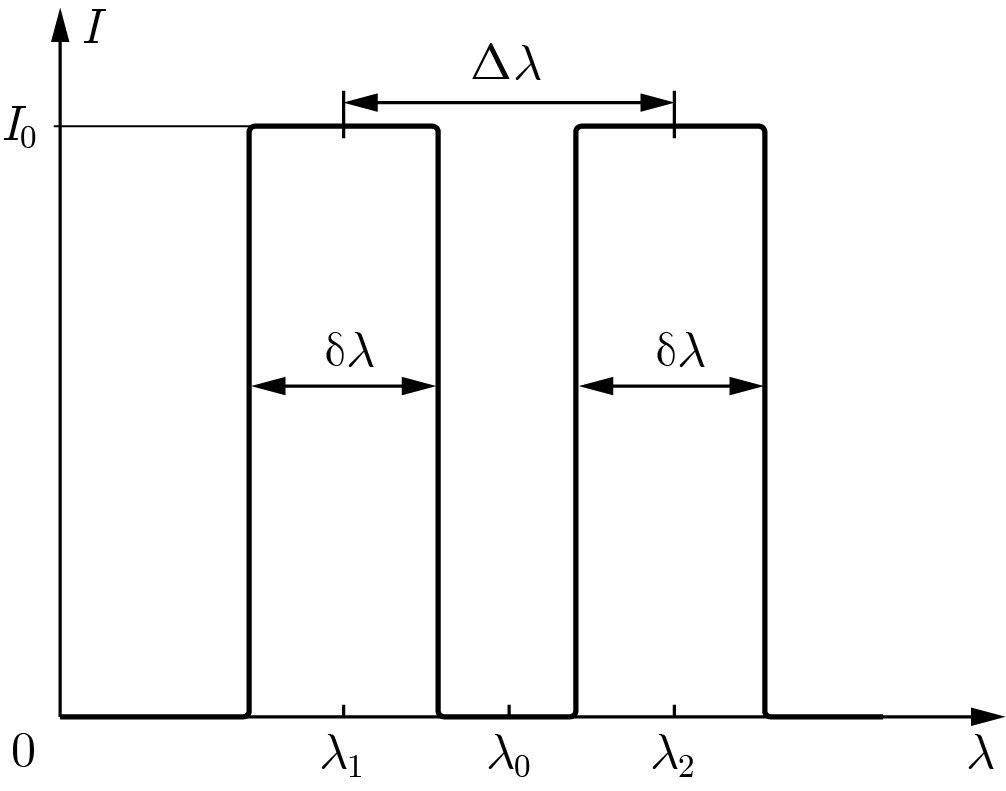
При прохождении через поляризатор $P$ естественный свет преобразуется в линейно-поляризованный свет, плоскость поляризации параллельна оси поляризатора. В этой части задачи будем рассматривать только монохроматическое излучение.
A2
0.40
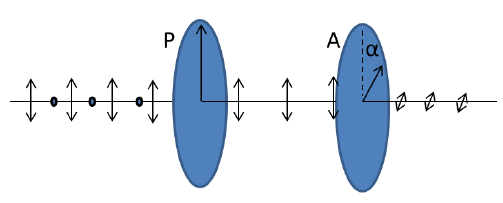
Поляризатор и анализатор расположены перпендикулярно друг другу, и свет не проходит через анализатор. Если между двумя элементами поместить третий поляризатор $P'$, свет начинает проходить через анализатор. Найдите интенсивность $I$ прошедшего света через интенсивность падающего света $I_0$ и угол $\alpha$, который составляет ось поляризатора $P'$ с осью поляризатора $P$. Найдите максимальную интенсивность прошедшего света $I'$ и угол $\alpha'$, при котором она достигается.
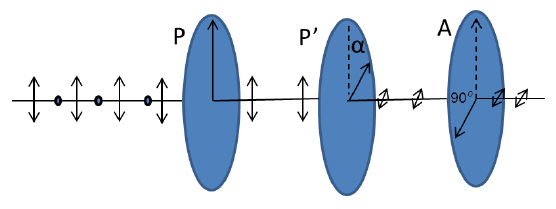
Заменим теперь поляризатор $P'$ на двулучепреломляющий кристалл. В таком кристалле падающий луч делится на два. Один из них распространяется с одинаковой скоростью в любом направлении, так называемый «обыкновенный» (ordinary) луч, а другой распространяется с разными скоростями в разных направлениях, «необыкновенный» (extraordinary) луч. На рисунке показаны волновые фронты для обыкновенного луча (сферический) и для необыкновенного (эллипсоидальная) для точечного источника, расположенного в кристалле. Направление, в котором лучи распространяются с одинаковой скоростью, называется осью кристалла. Показатель преломления для обыкновенного луча равен $n_o$, а показатель преломления для необыкновенного луча зависит от направления, и его значение находится между $n_o$ и $n_e$.
A3
0.30
Рассмотрим кристалл, грани которого параллельны оси кристалла. Линейно-поляризованный свет нормально так падает на поверхность кристалла. Два луча будут распространяться в одном направлении, но с разными скоростями. Они линейно поляризованы во взаимно перпендикулярных направлениях. На выходе из кристалла между двумя лучами появляется фазовый сдвиг. Выразите этот фазовый сдвиг $\delta$ через показатели преломления $n_o$ и $n_e$, а также длину волны излучения $\lambda$ и толщину кристалла $d$.
A4
1.20
Пусть амплитуды обеих волн (обыкновенной и необыкновенной), одинаковы и равны $E$. Найдите соотношение между напряженностью электрического поля необыкновенной волны $E_e$, напряженностю электрического поля обыкновенной волны $E_o$ и фазовым сдвигом $\delta$. Проанализируйте случаи, когда сдвиг фазы $\delta$ принимает значения $\delta = 2\pi k, \delta=(2k+1)\pi, \delta=k\pi+\frac{\pi}{2}, k\in Z.$ Для каждого из случаев укажите поляризацию света, выходящего из кристалла.
Некоторые вещества под действием электрического поля приобретают свойства одноосного кристалла, причем оптическая ось оказывается направлена по полю. Электрооптический эффект заключается в изменении значения показателя преломления среды в электрическом поле. Если показатель преломления линейно зависит от напряженности приложенного электрического поля, это явление называется эффектом Поккельса. Т.е. $n(E)=n_0+aE$, причем $aE\ll n_0$. Значение постоянной $a=-\cfrac{1}{2}rn_0^3$, где $r$~— коэффициент Поккельса. Для прикладных исследований удобно использовать следующую величину: $\eta=\cfrac{1}{n^2}$.
B2
0.50
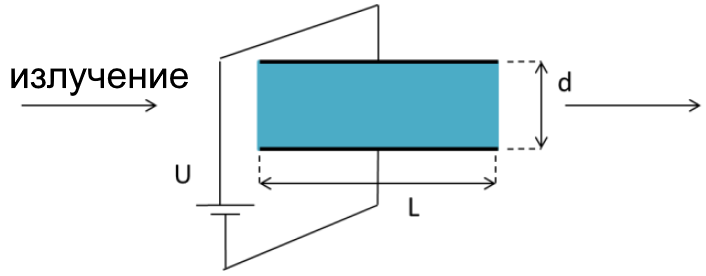
Вариант ячейки Поккельса показан на рисунке. Показатель преломления вещества в отсутствие поля $n_0$, размеры ячейки $L$ и $d$. длина волны используемого излучения $\lambda$, и коэффициент Поккельса $r$. Какое напряжение нужно приложить, чтобы ячейка вносила разность фаз $\delta\phi=\phi-\phi_0=\pi$, где $\phi_0$~— фазовый сдвиг при отсутствии поля, $\phi$~— в присутствии поля.
B3
1.00
Пусть для некоторого анизотропного вещества два показателя преломления зависят от напряженности поля следующим образом $n_e=n_{e0}-\cfrac{1}{2}r_en_{e0}^3E$ и $n_o=n_{o0}-\cfrac{1}{2}r_on_{o0}^3E$. Кристалл был вырезан так, что в отсутствии поля на выходе получался линейно-поляризованный свет. Какое минимальное напряжение нужно приложить, чтобы получить на выходе линейно-поляризованный свет, поляризация которого повернута на $90^\circ$ относительно той, которая получается на выходе при отсутствии напряжения?
Если зависимость показателя преломления от напряженности поля носит квадратичный характер, то этот эффект называется эффектом Керра. И для одноосного кристалла выполняется следующее соотношение между показателями преломления обыкновенной и необыкновенной волной: $n_e-n_o=\lambda BE^2$, где $B$~— постоянная Керра.
B4
2.00
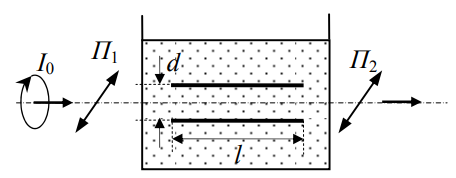
На рисунке изображена кювета с нитробензолом (который проявляет эффект Керра), в которой расположен конденсатор. С обеих сторон к кювете примыкают два идеальных поляроида, разрешенные направления которых параллельны и направлены под углом $\alpha=45^\circ$ к направлению поля в конденсаторе. Пластины конденсатора имеют длину $l=5~\text{см}$, расстояние между ними $d=5~\text{мм}$. К конденсатору приложено напряжение $U=2910~\text{В}$. Определите интенсивность $I$ света на выходе второго поляроида, если на первый поляроид падает свет, поляризованный по кругу с интенсивностью $I_0$. Постоянная Керра для нитробензонла равна $B=2.2\cdot 10^{-12}~\text{м/В}^2$.
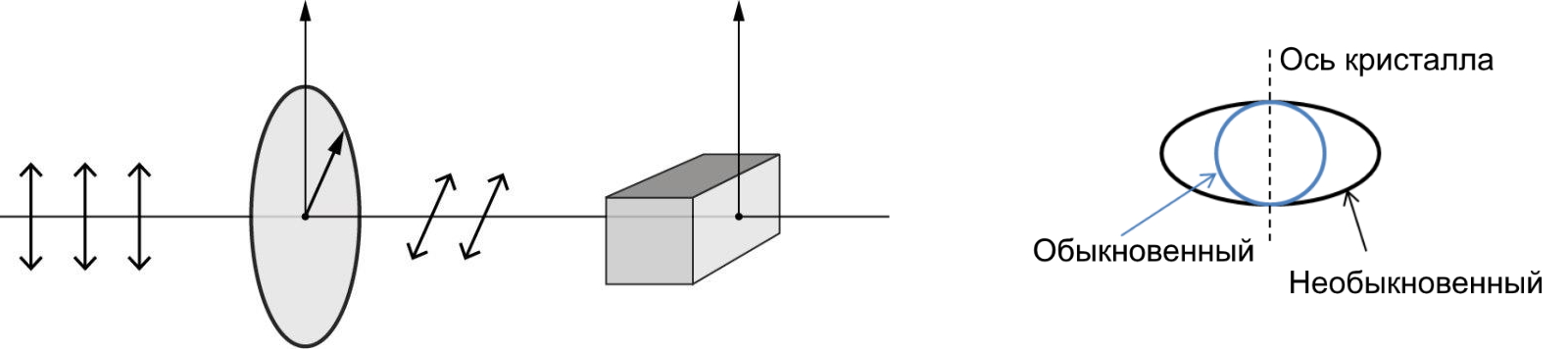
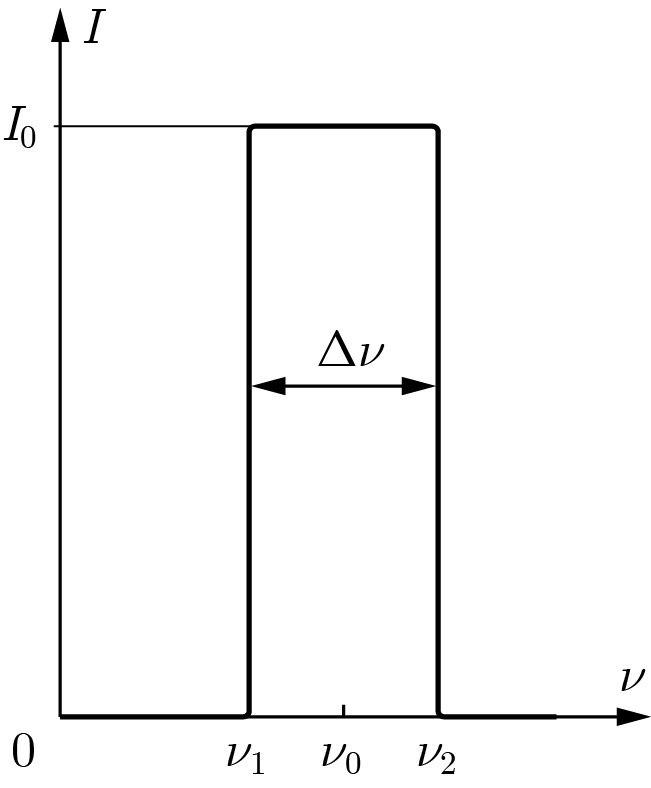
Интерференционная двулучевая схема освещается красной линией кадмия $\lambda_0=6438,8~\text{А}$, спектральной ширины $\lambda=1.2\cdot 10^-3~\text{А}$. В частотном спектре интенсивность излучения представляет собой прямоугольник. Пусть $L$~— разность оптических путей между двумя волнами, которые интерферируют в некоторой точке наблюдения $M$, а $p\equiv L/\lambda_0$~— порядок интерференции в этой точке.
Эксперимент повторяется. Теперь интерференционная схема освещается дуплетом натрия ($\lambda_1=5890~\text{А}, \lambda_2=5896~\text{А}, \delta\lambda=0.11~\text{А}$). Обозначим $\lambda_0$~— среднее арифметческое длин волн $\lambda_1$ и $\lambda_2$.