Вам может понадобиться интеграл:
$$\int \frac{dx}{\sqrt{a^2 + x^2}} = \mathrm{arth} \frac{x}{\sqrt{a^2+x^2}} + C,$$
где $\mathrm{arth} \,y$ обозначает обратный гиперболический тангенс числа $y$.

A1  ^0.50 Диск радиусом $R$ заряжен поверхностной плотностью заряда $\sigma_R$. Определите потенциал $\varphi(y)$ в точке на оси на расстоянии $y$ от центра диска. Потенциал равен нулю на бесконечности.

A2  ^1.00 Два таких диска радиусом $R$ заряжены поверхностной плотностью заряда $\sigma_R>0$ находятся параллельно друг другу. Расстояние между центрами дисков равно $2L$, центры находятся на оси дисков. В положении равновесия находятся заряд $q$ массой $m$, который может двигаться только вдоль оси дисков. Определите угловую частоту $\omega_1$ колебаний такого заряда. Какой знак заряда?

A3  ^1.00 Теперь этот заряд может двигаться только в перпендикулярном направлении. Выразите угловую частоту $\omega_2$ колебаний в таком случае через $\omega_1$. Какой теперь знак заряда?

B1  ^1.00 Боковая поверхность цилиндра радиусом $R$ и длиной $L$ заряжена поверхностной плотностью заряда $\sigma_L$. Определите потенциал в точке на оси на расстоянии $z$ от центра одного из оснований цилиндра. Потенциал равен нулю на бесконечности.

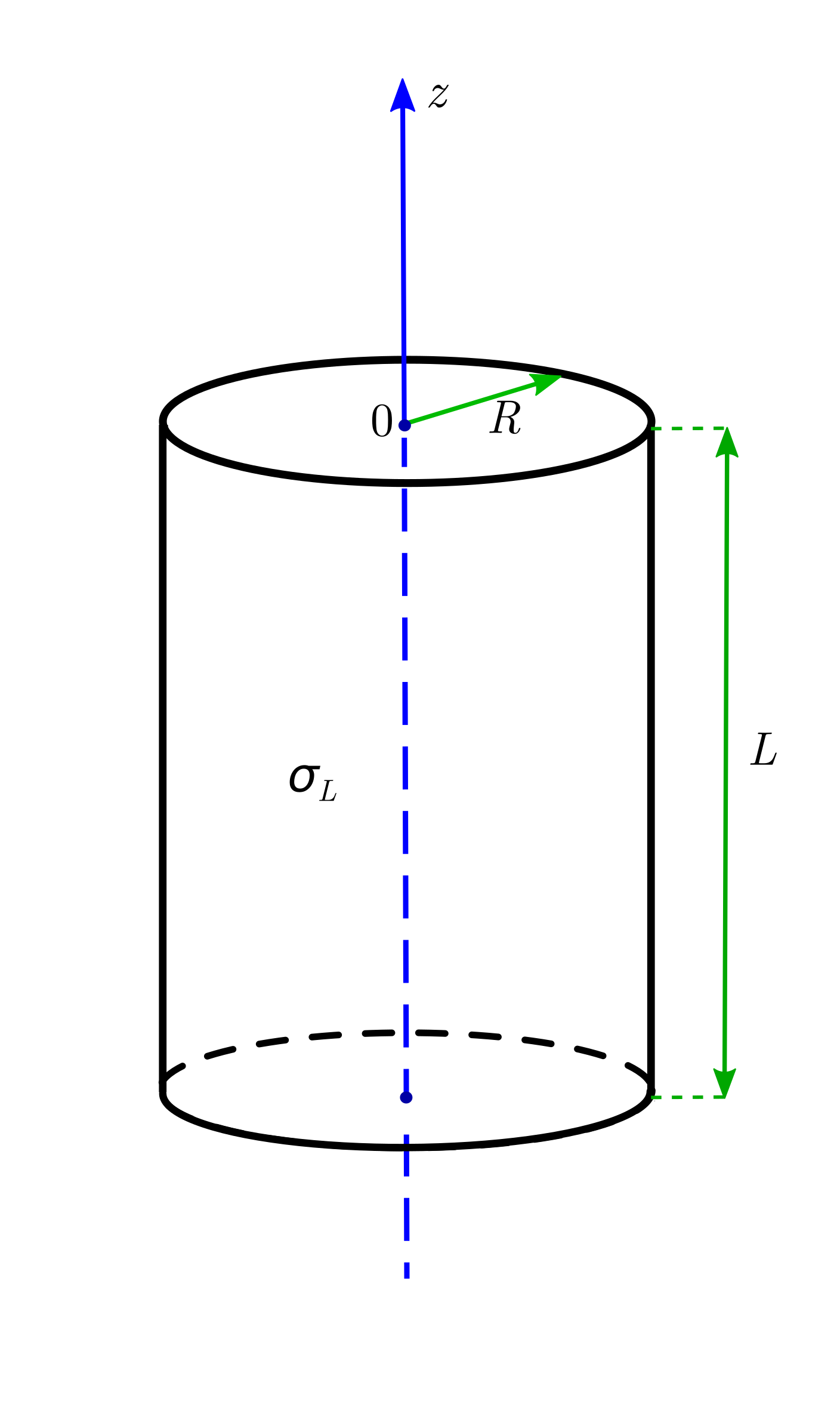
B2  ^1.00 Два таких цилиндра (радиусом $R$ и длиной $L$, поверхность заряжена поверхностной плотностью заряда $\sigma_L>0$) поставлены рядом вплотную и имеют общую ось. В положении равновесия находятся заряд $q$ массой $m$, который может двигаться только вдоль оси цилиндров. Определите угловую частоту $\omega_3$ колебаний такого заряда. Какой знак заряда?

B3  ^0.50 Теперь этот заряд может двигаться только в перпендикулярном направлении. Выразите угловую частоту $\omega_4$ колебаний в таком случае через $\omega_3$. Какой теперь знак заряда?

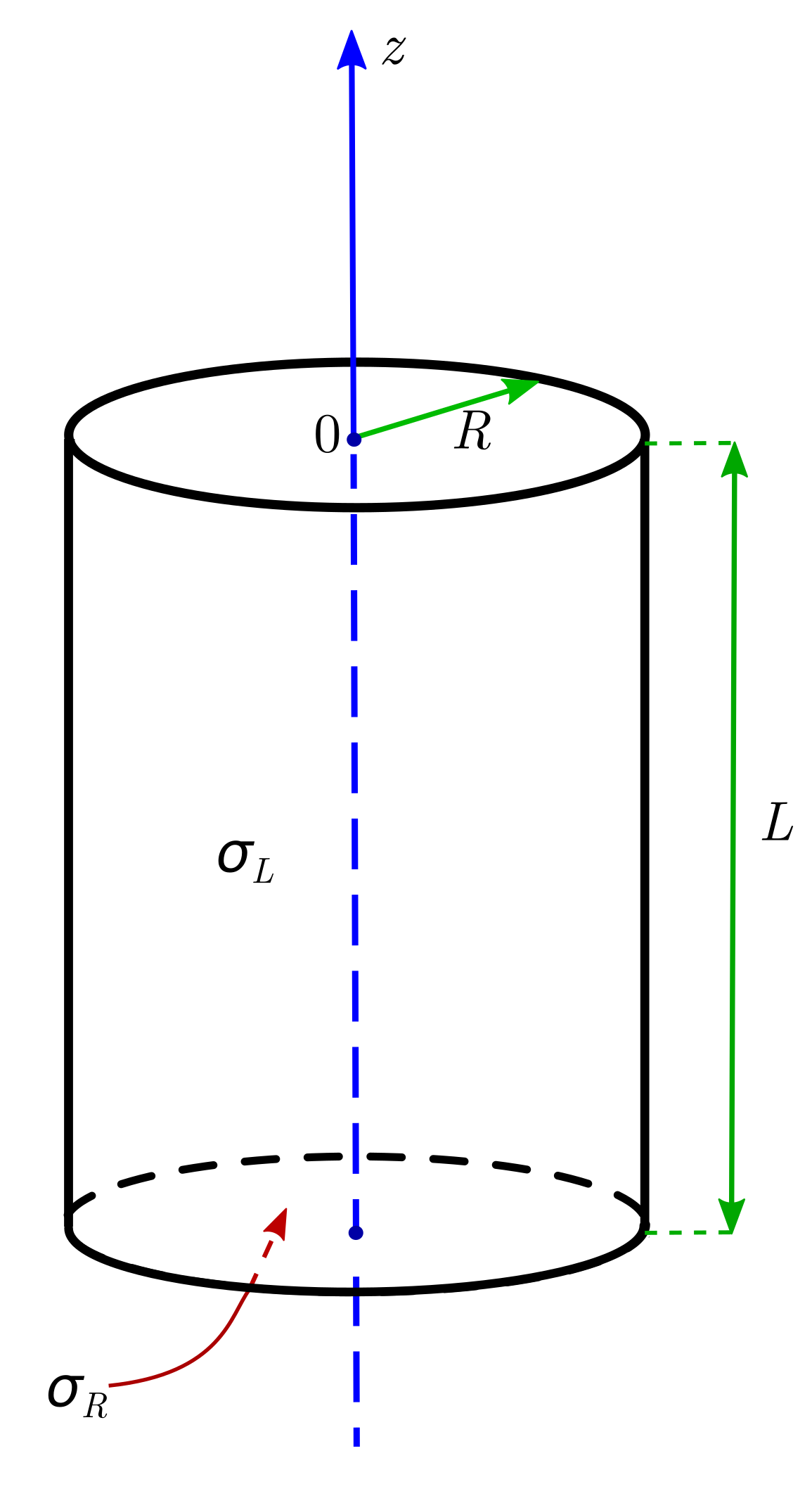
С1  ^1.50 Заряженный цилиндр радиусом $R$ высотой $L=40R/9$ состоит из боковой поверхности и одного основания. Поверхностная плотность заряда боковой поверхности $\sigma_L$, основания $\sigma_R$. Если поместить точечный заряд в центр противоположного основания, то он окажется в положении равновесия. Определите отношение $\sigma_L/\sigma_R$.

С2  ^2.50 Заряженный цилиндр радиусом $R=28b$ высотой $L=45b$ состоит из боковой поверхности и одного основания. Заряд боковой поверхности $\sigma_L=-8\sigma_0$, заряд основания $\sigma_R=25\sigma_0>0$. На оси этой системы помещают частицу c зарядом $q>0$. Оцените численно координаты $z$ (в единицах $b$) положений равновесия если частица может двигаться только вдоль оси. Координата $z$ отсчитывается как на картинке.
Сделайте это максимально точно, однако, достаточно с точностью 1%. Ответы попадающие в 1% от правильного получат полный балл.

С3  ^1.00 В условиях предыдущего пункта частицу поместили в ближайшее к цилиндру положение равновесия, её масса $m$. Определите угловую частоту $\omega$ малых колебаний частицы.