В данной работе вам потребуется определить радиус выданной нити тремя различными способами. Так как измеряемые эффекты достаточно тонкие, далее вам потребуется постичь дзен.

Оборудование

1. Катушка с ниткой
2. Две одинаковых гайки
3. Штатив с лапкой и муфтой
4. Линейка
5. Секундомер
6. Весы
7. Клейкая масса
8. Мерная лента
9. Ножницы и скотч по требованию

Часть A. Геометрия винтовых линий (1 балл)

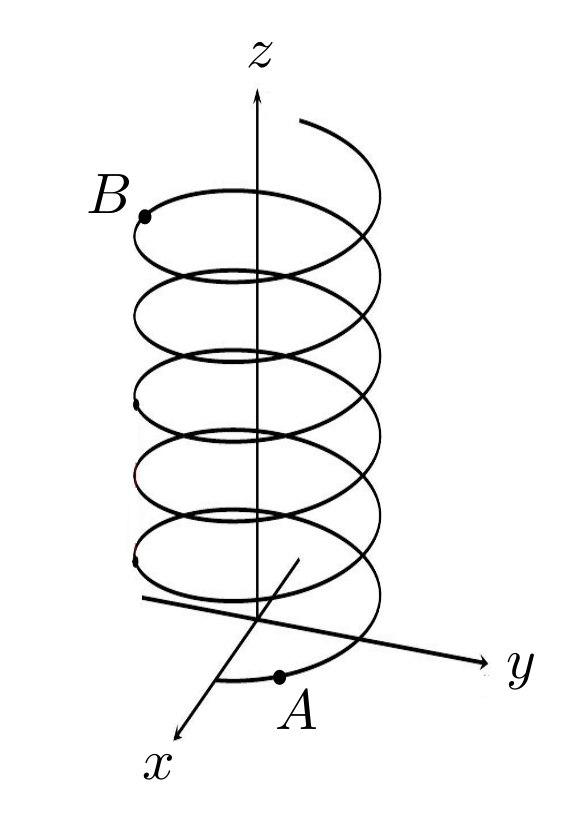
Винтовой линией на поверхности цилиндра радиуса $R$ называется такая кривая, что в любой её точке касательная к ней составляет одинаковый угол с осью симметрии цилиндра (см. рис). Координаты $x$ и $y$ точек винтовой линии определяются выражениями
$$x=R\cos(\varphi);~y=R\sin(\varphi)
$$
Во всех пунктах данной части длина кривой равняется $l$.

A1  ^0.20 Пусть кривая совершает один оборот вокруг цилиндра радиуса $R<\frac{l}{2\pi}$
(т.е $\varphi_B-\varphi_A=2\pi$)
Найдите угол между касательной к кривой и осью симметрии цилиндра.

A2  ^0.40 Пусть $\varphi_B-\varphi_A=\Delta{\varphi}$.
Выразите $z_B-z_A$ через $l$, $R$ и $\Delta{\varphi}$

A3  ^0.40 Для $\frac{R\Delta{\varphi}}{l}\ll1$ покажите, что
$$z_B-z_A=l-\frac{(R\Delta{\varphi})^2}{2l}$$

Полученные формулы пригодятся в дальнейших частях задачи.

Часть В. Подготовительная (4 балла)

B1  ^0.10 Измерьте массу гайки $m$.

B2  ^0.90 Измерьте радиус нити $r_1$ методом рядов.

B3  ^3.00 Измерьте момент инерции гайки относительно её главной оси.
Считайте, что $g = 9,8$ $\text{м}/\text{с}^2$.

Часть C. Крутим гайку ( баллов)

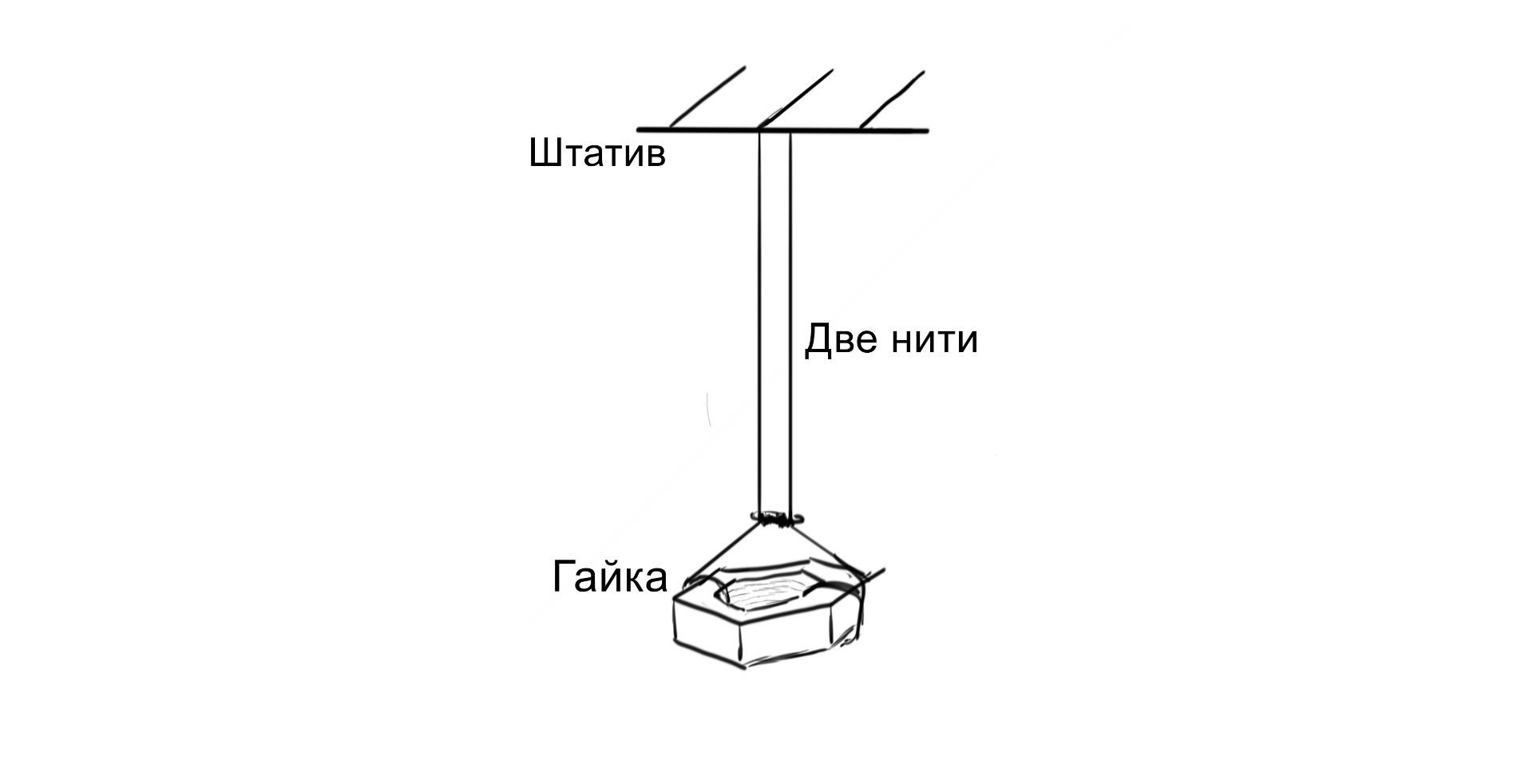
Соберите установку по схеме ниже. Длина нитей должна быть равна 30-45 см. В верхней точке расстояние между нитями должно быть порядка 1 мм или меньше. Точка скрепления нитей должна быть зафиксирована. Обратите внимание, что в положении равновесия нити закручены на какой-то угол.

С1 Запишите расстояние $L$ от точки подвеса до точки скрепления для вашей установки.

С2  ^1.70 При закручивании нитей на угол $\varphi$ гайка поднимается на высоту $h$. Снимите зависимость $h(\varphi)$ в максимально широком диапазоне (до углов порядка $500\pi$), закручивая гайку против часовой стрелки, если смотреть на на неё сверху вниз. В дальнейшем будем называть это направление закрутки правым. Следите за тем, чтобы отрезки нитей ниже точки скрепления не перекручивались. На нитях не должны появляться узелки и катышки.

С3  ^1.10 Снимите аналогичную зависимость для закручивания в другую сторону. Убедитесь в асимметрии установки.

ВАЖНО: Все дальнейшие измерения проводите при закручивании гайки против часовой стрелки, если смотреть на установку сверху.

ВАЖНО: при построении всех дальнейших теоретических зависимостей считайте нити нерастяжимыми.

C4  ^0.30 Выведите теоретическую зависимость $h(\varphi)$. Пользуясь этим, линеаризуйте зависимость, полученную в пункте С2.

C5  ^1.20 Для правой закрутки нити постройте график зависимости $h(\varphi)$ в координатах, в которых он является линейным. Из углового коэффициента еще раз определите радиус нити $r_2$.

С6  ^0.70 Получите теоретическую зависимость $\tau$ от параметров установки, где $\tau(h)$ - время, за которое гайка останавливается, если её отпустить с высоты $h$.

С7  ^1.00 Для правой закрутки экспериментально получите зависимость $\tau(h)$.

С8  ^2.50 Снимите зависимость $\tau(L)$. Постройте линеаризованный график.

C9  ^1.20 Модулем кручения $f$ однородного стержня называют коэффициент пропорциональности в формуле $M = f \cdot \varphi$, где $M$ - закручивающий момент сил, приложенных к основанию стержня, $\varphi$ - угол поворота основания стержня. Определите коэффициент $C$ в зависимости $f = C/L$, где $f$ - собственный модуль кручения одной нити, $L$ - длина нити. Опишите метод. Оцените отношение $\frac{C}{mgr^2}$. Убедитесь, что рассмотренный эффект почти не влияет на полученные результаты.

C10  ^0.30 Заметьте, что гайка раскручивается до неразличимых глазом угловых скоростей. Оцените по порядку, с какой максимальной угловой скоростью она вращается.

Часть D. Крутим линейку (5 баллов)

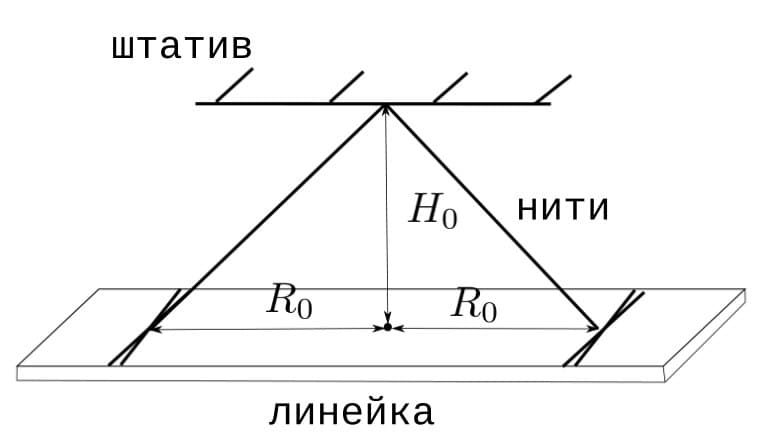
В этой части задачи используется экспериментальная установка, изображенная на рисунке ниже. Линейка подвешена на двух нитях параллельно полу, причём расстояние между концами нити на штативе мало, а на линейке - велико. Обозначим как $\tau'(\varphi)$ время, нужное системе, закрученной на угол $\varphi$, чтобы снова остановиться.

Перейдем к построению теоретической модели. Пусть линейка изначально повернута на угол $\varphi_0$ от положения равновесия.

D1  ^1.20 Считая известным, что при отклонении линейки на угол $\varphi$ от положения равновесия изменение её высоты представимо в виде
$$h=A{\varphi},
$$
выразите $A$ через $R_0$,$H_0$ и $r$.

D2  ^0.80 Получите теоретическую зависимость $\tau'(\varphi_0)$, где $\tau'$ - время от начала движения линейки до момента ее первой остановки, $\varphi_0$ - начальный угол закручивания нитей.

Соберите установку, изображенную на рисунке. Используйте $R_0\approx 24$ см, $H_0 < 40$ см.

D3  ^1.50 Снимите зависимость $\tau'(\varphi_0)$, где $\tau'$ - время от начала движения линейки до момента ее первой остановки, $\varphi_0$ - начальный угол закручивания нитей. Измерения проводите в диапазоне $\varphi_0 \in [\pi; 10\pi]$.

D4  ^1.50 Постройте линеаризованный график и в третий раз определите радиус нити $r_3$.