Работа над повышением КПД паросиловых установок является важной частью снижения экономических затрат на поддержание электростанций. Развитие данной отрасли всегда упиралось в сложности технической реализации установок, а также в переход реального газа в жидкую фазу. Инженеры сформулировали следующие требования к веществам, используемым в циклах:

1. Удельная теплоёмкость вещества в жидкой фазе должна быть наименьшей;
2. Критическая точка вещества должна достигаться при высокой температуре и сравнительно невысоком давлении;
3. Давление насыщенного пара при наименьшей температуре не должно быть слишком низким;
4. Вещество должно быть легкодоступным.

Ограничения на теплоёмкость в жидкой фазе и температуру вещества в критической точке понятны из теоретических соображений, а создание камеры, выдерживающей высокое давление, и вакуумного конденсатора, поддерживающего низкое давление, являются сложными с технической точки зрения задачами. В настоящее время неизвестны вещества, удовлетворяющие всем перечисленным требованиям, в связи с чем была предложена идея бинарных циклов — использовать преимущества одного теплоносителя при высоких температурах, а другого — при низких. Бинарные циклы обладают большим КПД, чем циклы с одним из рассматриваемых веществ. Идея бинарных циклов заключается в том, чтобы между двумя веществами, находящихся в разных сосудах, происходил теплообмен. Это позволяет реализовать два цикла одновременно, избегая при этом вынужденного подведения тепла к одному из рабочих тел в процессе теплообмена.

Цикл Ренкина $1-2-3-4-1$ является одним из наиболее используемых в бинарных циклах. Он состоит из следующих процессов:

1. $1-2$ - адиабатическое расширение;
2. $2-3$ - изотермическое охлаждение (отведение теплоты);
3. $3-4$ - адиабатическое сжатие;
4. $4-1$ - изобарное нагревание.

Далее, если это не оговорено отдельно, для циклов Ренкина придерживайтесь введённых обозначений. В частях $\mathrm{A}$ и $\mathrm{B}$ анализируются циклы Ренкина с рабочим веществом в виде идеального газа и воды соответственно, а в частях $\mathrm{C}$ и $\mathrm{D}$ — соответственно бинарный газово-пароводяной цикл (будет описан отдельно) и бинарный цикл Ренкина с рабочими телами в виде воды и ртути в обоих случаях.

Часть A. Цикл Ренкина с идеальным газом (2.0 балла).

Рассмотрим цикл Ренкина с идеальным многоатомным газом. Абсолютные температуры в точках $1$, $2$ и $4$ обозначим за $T_1$, $T_2$ и $T_4$ соответственно.
Введём величины $\alpha$ и $\beta$, определяющие соотношение между температурами и давлениями в точках $2$ и $4$:
$$\alpha=\cfrac{T_4}{T_2}\qquad \beta=\cfrac{p_4}{p_2}
$$

A1  ^0.70 Выразите отведённое от газа за цикл количество теплоты $Q_-$ через $T_1$, $T_2$, $T_4$, $R$, количество вещества газа $\nu$ и показатель адиабаты $\gamma$.

A2  ^0.80 Выразите отношение $T_1/T_4$ через $\alpha$, $\beta$ и $\gamma$.

A3  ^0.50 Получите выражение для КПД цикла $\eta_1$. Ответ выразите через $\alpha$, $\beta$ и $\gamma$.
Найдите численное значение $\eta_1$ при $p_2=15~\text{кПа}$, $p_4=60~\text{кПа}$, $T_2=340~\text{К}$ и $T_4=400~\text{К}$.

Как уже говорилось ранее, реальным газам свойственен переход в жидкую фазу. В соответствии с требованиями инженеров к рабочим веществам бинарных циклов, опытным путём было установлено, что вода и ртуть компенсируют недостатки друг друга. Вода не удовлетворяет условию низкой теплоемкости в жидкой фазе и обладает низкой критической температурой, но удовлетворяет условию не слишком низкого значения давления в конденсаторе. Ртуть же имеет невысокое давление насыщенных паров при высоких температурах и высокую критическую температуру при сравнительно невысоком давлении, но очень низкое давление насыщенных паров в конденсаторе. В процессе теплообмена вода при температурах, близких к критической, обменивается теплом с ртутью при сравнительно невысоких для ртути температурах (порядка $200-300^\circ\mathrm{C}$). Во всех последующих частях задачи рассматриваются циклы с водой и ртутью. Индексами $\text{''(р)''}$ и $\text{''(в)''}$ будем характеризовать ртутный и водяной циклы соответственно.

Используйте обозначения, численные данные и приближения, описанные ниже:

1. Универсальная газовая постоянная $R=8{,}31~\text{Дж}/(\text{моль}\cdot{\text{К}})$;
2. Показатель адиабаты $C_p/C_V=\gamma$;
3. Удельная теплоёмкость воды в жидкой фазе равна $c_\text{в}=4190~\text{Дж}/(\text{кг}\cdot{\text{К}})$ и постоянна;
4. Молярная масса воды равна $\mu_\text{в}=18{,}02~\text{г}/\text{моль}$;
5. Удельная теплоёмкость ртути в жидкой фазе равна $c_\text{р}=140~\text{Дж}/(\text{кг}\cdot{\text{К}})$ и постоянна;
6. Молярная масса ртути равна $\mu_\text{р}=200{,}59~\text{г}/\text{моль}$;
7. Всегда считайте пар (как насыщенный, так и ненасыщенный) ртути идеальным одноатомным газом.

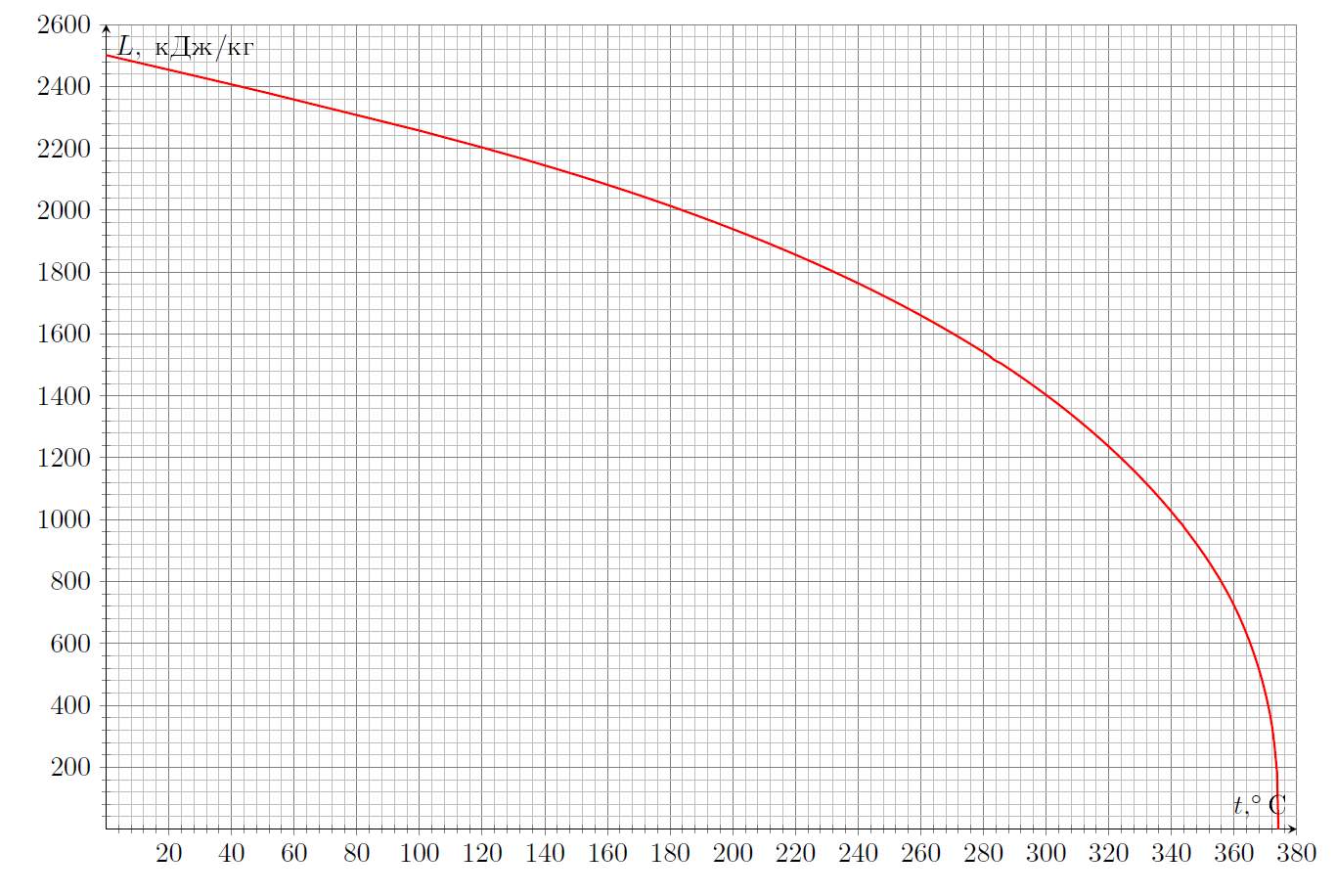
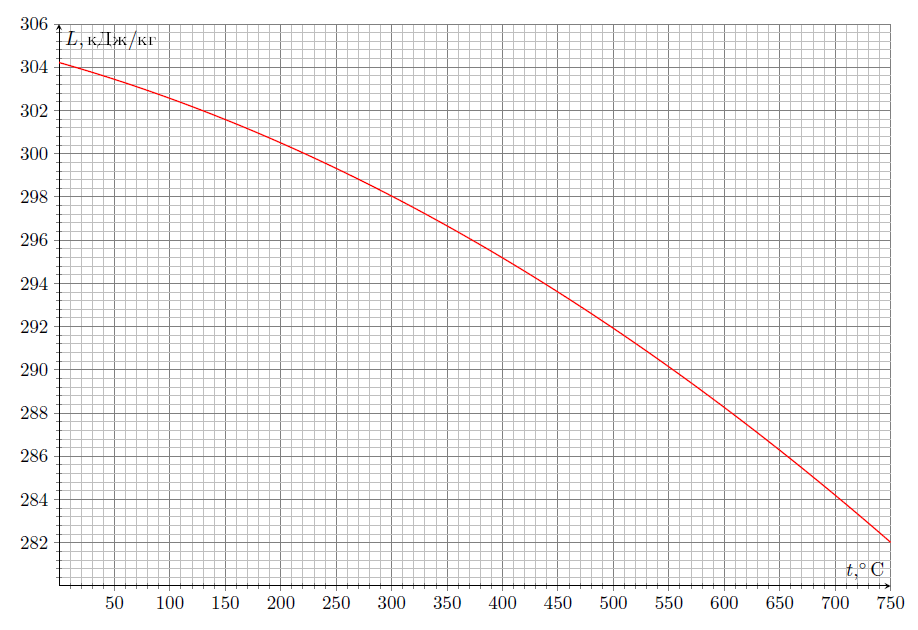
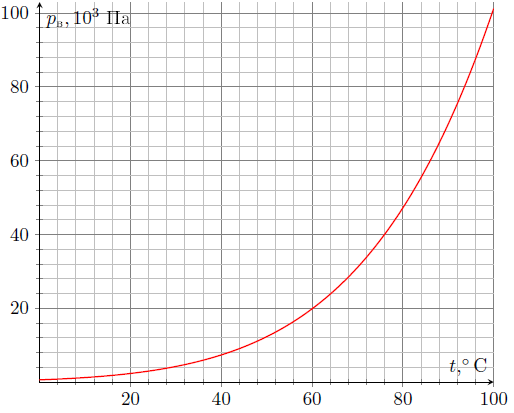
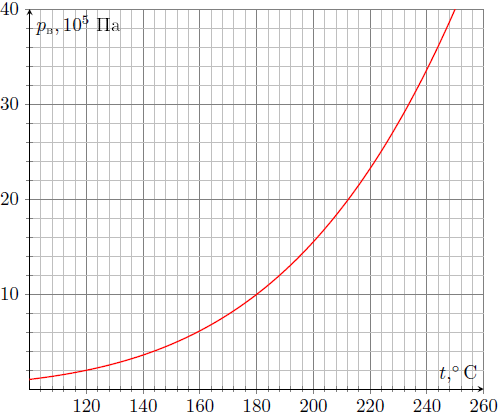
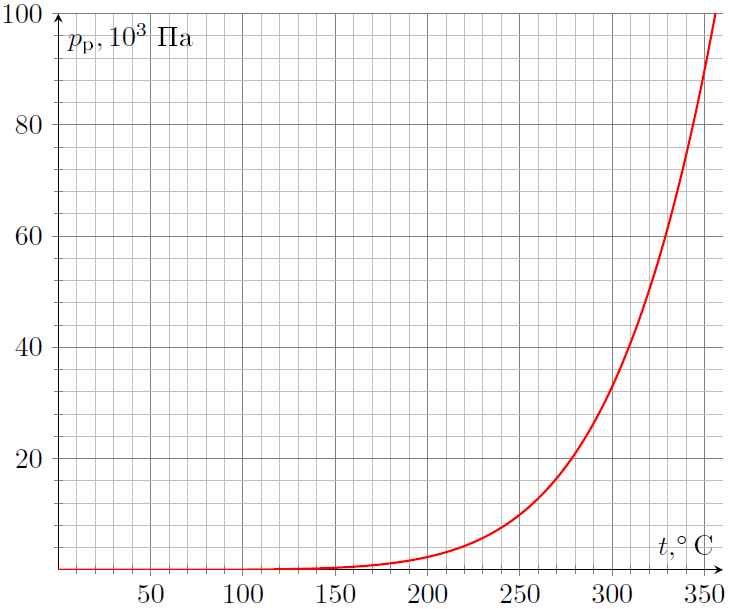
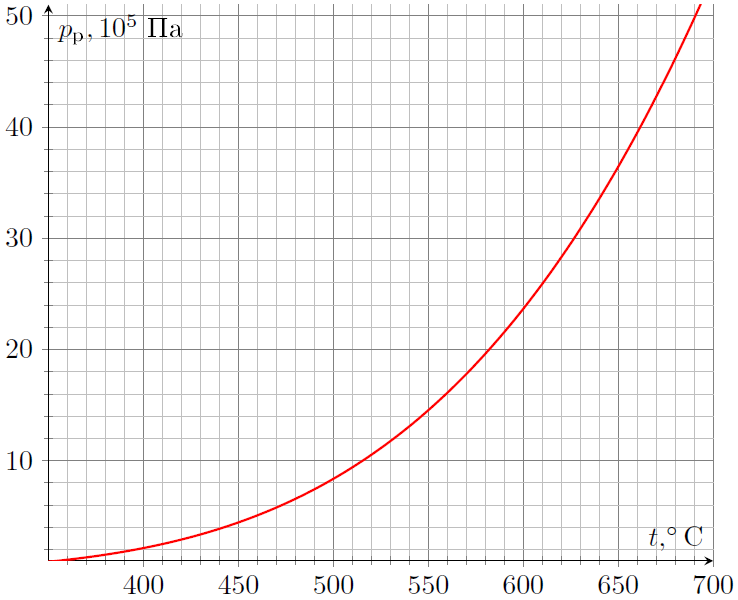
Ниже приведены зависимости удельной теплоты парообразования ртути и воды от температуры, а также (на двух графиках, в областях сравнительно малых и больших давлений) зависимости давлений насыщенных паров ртути и воды от температуры:

Часть B. Бинарный газово-пароводяной цикл (2.5 балла).

В данной части задачи рассматривается бинарный цикл, представляющий собой комбинацию газового и пароводяного циклов.

Примечание: в данной части задачи и ртуть, и вода всё время целиком находятся в газообразной фазе.

Газовый цикл $a_\text{(р)}-b_\text{(р)}-c_\text{(р)}-d_\text{(р)}-a_\text{(р)}$ для ртутного пара состоит из следующий процессов:

1. $a_\text{(р)}-b_\text{(р)}$ — адиабатическое расширение паров ртути;
2. $b_\text{(р)}-c_\text{(р)}$ — изобарное сжатие паров ртути до состояния насыщения;
3. $c_\text{(р)}-d_\text{(р)}$ — адиабатическое сжатие паров ртути;
4. $d_\text{(р)}-a_\text{(р)}$ — изотермическое расширение паров ртути.

Пароводяной цикл $a_\text{(в)}-b_\text{(в)}-c_\text{(в)}-d_\text{(в)}-a_\text{(в)}$ состоит из следующий процессов:

1. $a_\text{(в)}-b_\text{(в)}$ — адиабатическое расширение перегретого (до температуры, выше критической) водяного пара;
2. $b_\text{(в)}-c_\text{(в)}$ — изотермическое сжатие водяного пара до состояния насыщения;
3. $c_\text{(в)}-d_\text{(в)}$ — адиабатическое сжатие водяного пара;
4. $d_\text{(в)}-a_\text{(в)}$ — изобарное нагревание водяного пара.

Примечание: в данной части задачи считайте пар воды идеальным многоатомным газом, теплоёмкость которого $C_V$ не зависит от температуры. Цикл проводится так, что соответствующие температуры связаны следующим образом: $$t_{a(\text{р})}=t_{d(\text{р})}=t_1\quad t_{b(\text{в})}=t_{c(\text{в})}=t_2\quad t_{b(\text{р})}=t_{a(\text{в})}=t_3\quad t_{c(\text{р})}=t_{d(\text{в})}=t_4 $$

Считайте известными следующие данные:
$$t_1=640^{\circ}\mathrm{C}\quad t_2=40^{\circ}\mathrm{C}\quad t_3=470^{\circ}\mathrm{C}\quad t_4=230^{\circ}\mathrm{C}
$$

В изобарных процессах между ртутью и водяным паром происходит теплообмен, так что количество теплоты, отведённое от паров ртути на участке $b_\text{(р)}-c_\text{(р)}$ равно количеству теплоты, подведённому к парам воды на участке $d_\text{(в)}-a_\text{(в)}$:
$$-Q_{bc(\text{р})}=Q_{da(\text{в})}
$$

B1  ^0.50 Найдите отношение масс ртути и воды $m_\text{(р)}/m_\text{(в)}$, участвующих в цикле.

B2  ^0.40 Используя графики зависимости давления насыщенных паров ртути и воды от температуры, оцените значения давлений $p_{c\text{(р)}}$ и $p_{c\text{(в)}}$.

B3  ^0.80 Найдите КПД ртутного и водяного цикла $\eta_\text{(р)}$ и $\eta_\text{(в)}$ соответственно.

B4  ^0.80 Найдите КПД $\eta_\text{гп}$ бинарного газово-пароводяного цикла. Сравните его с $\eta_\text{(р)}$ и $\eta_\text{(в)}$.

В действительности, рассмотренный в части $\mathrm{B}$ бинарный цикл работает несколько иначе, поскольку теплоёмкость водяного пара зависит от температуры даже при постоянном давлении. Это связано как с тем, что насыщенный пар воды в действительности не является идеальным газом, так и с тем, что при повышении температуры газа вклад колебательного движения молекул в их кинетическую энергию перестаёт быть пренебрежимо малым, поэтому во всех последующих пунктах задачи считать пар воды идеальным газом уже нельзя. В действительности, молярная теплоёмкость пара воды $C_V$ зависит как от температуры, так и от давления, однако в рамках задачи при поиске элементарного количества теплоты $\delta{Q}$ зависимость $C_V$ от давления можно считать слабой, а также воспользоваться приближением изменения теплоёмкости скачком: $$C_V=\begin{cases} 3R\quad\text{при}\quad{t\leq{180^{\circ}C}}\\ 7R/2\quad\text{при}\quad{t>180^{\circ}C} \end{cases} $$ Примечание: поскольку теплоёмкость $C_V$ непрерывно зависит и от температуры, и от давления, любое интегральное уравнение состояния в координатах $pT$ (к примеру, уравнение Пуассона для адиабатического процесса), применённое при температуре, большей $t_{crit}\approx200^\circ$, будет давать существенную ошибку и приводить к весьма парадоксальным результатам! При температурах, меньших $t_{crit}$, можно с хорошей точностью пользоваться уравнениями состояния даже в координатах $pT$.

Часть C. Цикл Ренкина с промежуточным перегревом пара (2.0 балла).

В данной части задачи рассматривается пароводяной цикл Ренкина $1-2-3-4-5-6-1$. Полная последовательность процессов в цикле следующая:

1. $1-2$ — адиабатическое расширение водяного пара;
2. $2-3$ — изотермическое сжатие водяного пара до насыщения и последующая полная конденсация;
3. $3-4$ — адиабатическое сжатие воды (изменением температуры можно пренебречь);
4. $4-5$ — изобарное нагревание воды до температуры кипения;
5. $5-6$ — изобарное испарение воды;
6. $6-1$ — изобарное нагревание водяного пара.

Температура в точке $1$ равна $t_1=630^{\circ}\mathrm{C}$.
В точке $3$ давление в системе равно $p_3=16~\text{кПа}$, а в точке $4$ — $p_4=2{,}8~\text{Мпа}$.
Цикл проводится с массой $m_\text{в}=17~\text{кг}$.

C1  ^0.40 Найдите температуры системы в точках $2$, $3$, $4$, $5$ и $6$.

C2  ^0.60 Найдите количество теплоты $Q_+$, подведённое к системе за цикл.

C3  ^0.80 Найдите количество теплоты $Q_-$, отведённое от системы за цикл.

C4  ^0.20 Найдите работу газа $A$ за цикл и его КПД $\eta_2$.

Часть D. Бинарный цикл Ренкина (3.5 балла)

В данной части задачи мы рассмотрим бинарный цикл Ренкина для ртути и воды. Процессы ртутного цикла $a_\text{р}-b_\text{р}-c_\text{р}-d_\text{р}-e_\text{р}-a_\text{р}$:

1. $a_\text{р}-b_\text{р}$ — адиабатическое расширение ртутного пара;
2. $b_\text{р}-c_\text{р}$ — изотермическое сжатие ртутного пара с последующей полной конденсацией;
3. $c_\text{р}-d_\text{р}$ — адиабатическое сжатие жидкой фазы ртути (изменением температуры можно пренебречь);
4. $d_\text{р}-e_\text{р}$ — изобарное нагревание жидкой фазы ртути;
5. $e_\text{р}-a_\text{р}$ — полное испарение жидкой фазы ртути.

Процессы водяного цикла $a_\text{в}-b_\text{в}-c_\text{в}-d_\text{в}-e_\text{в}-f_\text{в}-a_\text{в}$:

1. $a_\text{в}-b_\text{в}$ — адиабатическое расширение водяного пара;
2. $b_\text{в}-c_\text{в}$ — изотермическое сжатие водяного пара до насыщения и последующая полная конденсация;
3. $c_\text{в}-d_\text{в}$ — адиабатическое сжатие воды (изменением температуры можно пренебречь);
4. $d_\text{в}-e_\text{в}$ — изобарное нагревание воды до температуры кипения;
5. $e_\text{в}-f_\text{в}$ — изобарное испарение воды;
6. $f_\text{в}-a_\text{в}$ — изобарное нагревание водяного пара.

Циклы проводятся согласованно и таким образом, что количество теплоты, отведённое от ртути на участке $b_\text{р}-c_\text{р}$ равно количеству теплоты, подведённому к парам воды на участке $e_\text{в}-f_\text{в}$:
$$-Q_{bc(\text{р})}=Q_{ef(\text{в})}
$$
Процессы $b_\text{р}-c_\text{р}$ и $e_\text{в}-f_\text{в}$ проводятся при одинаковой температуре.

Давления в точках $b_\text{в}$, $c_\text{в}$ и $e_\text{в}$ водяного цикла равны соответственно:
$$p_{b(\text{в})}=25~\text{кПа}\qquad p_{c(\text{в})}=88~\text{кПа}\qquad p_{e(\text{в})}=1{,}2~\text{МПа}
$$
Отношение масс ртути и воды $m_\text{р}/m_\text{в}=10{,}3$

D1  ^0.20 Найдите температуры в точках $b_\text{в}$, $c_\text{в}$, $d_\text{в}$, $e_\text{в}$, $f_\text{в}$ водяного цикла.

D2  ^1.00 Найдите температуру в точке $a_\text{в}$ водяного цикла.

D3  ^1.30 Найдите давление ртути на участке $d_\text{р}-e_\text{р}-a_\text{р}$.

D4  ^1.00 Найдите КПД бинарного цикла Ренкина с ртутью и водой $\eta_3$.